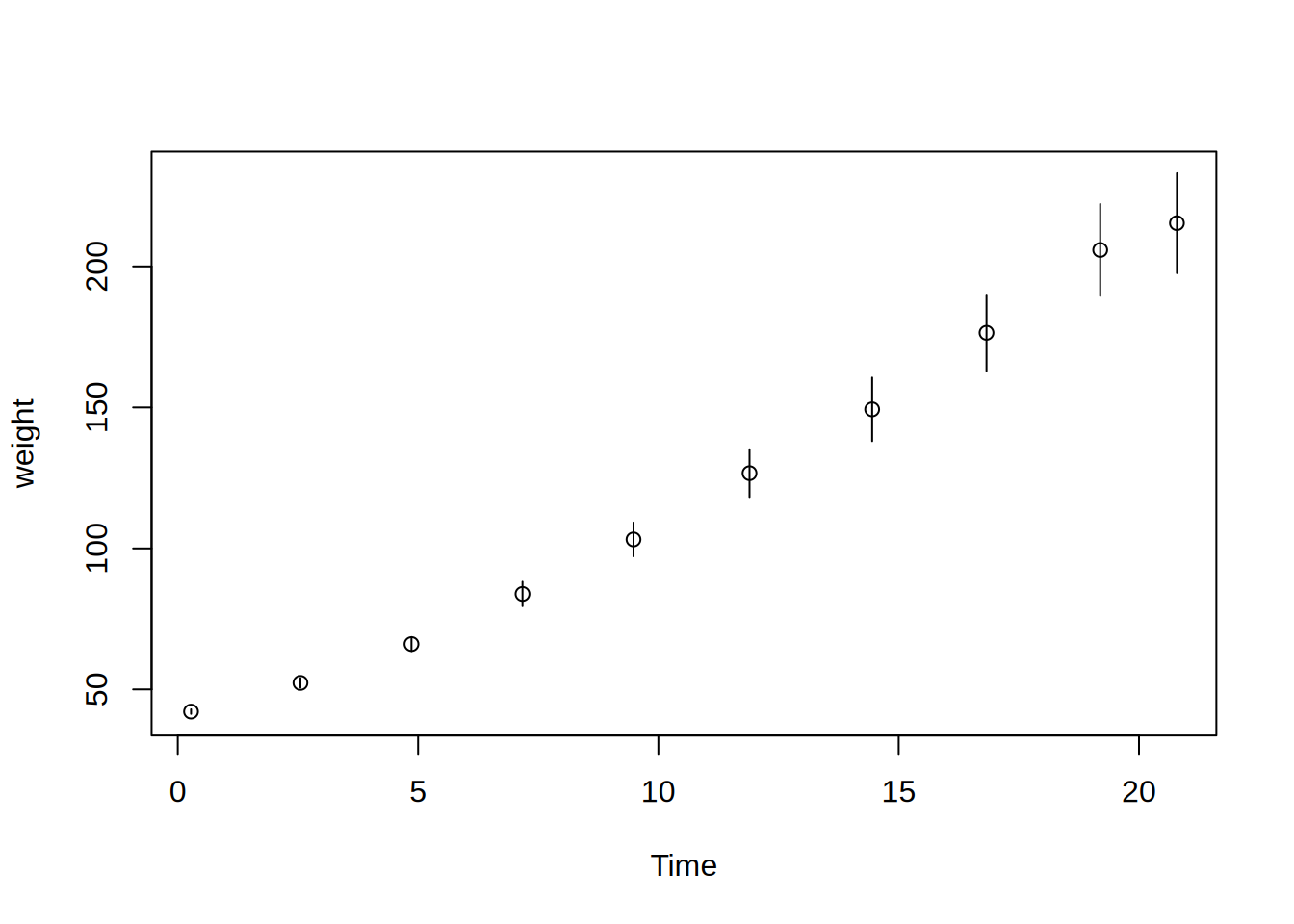
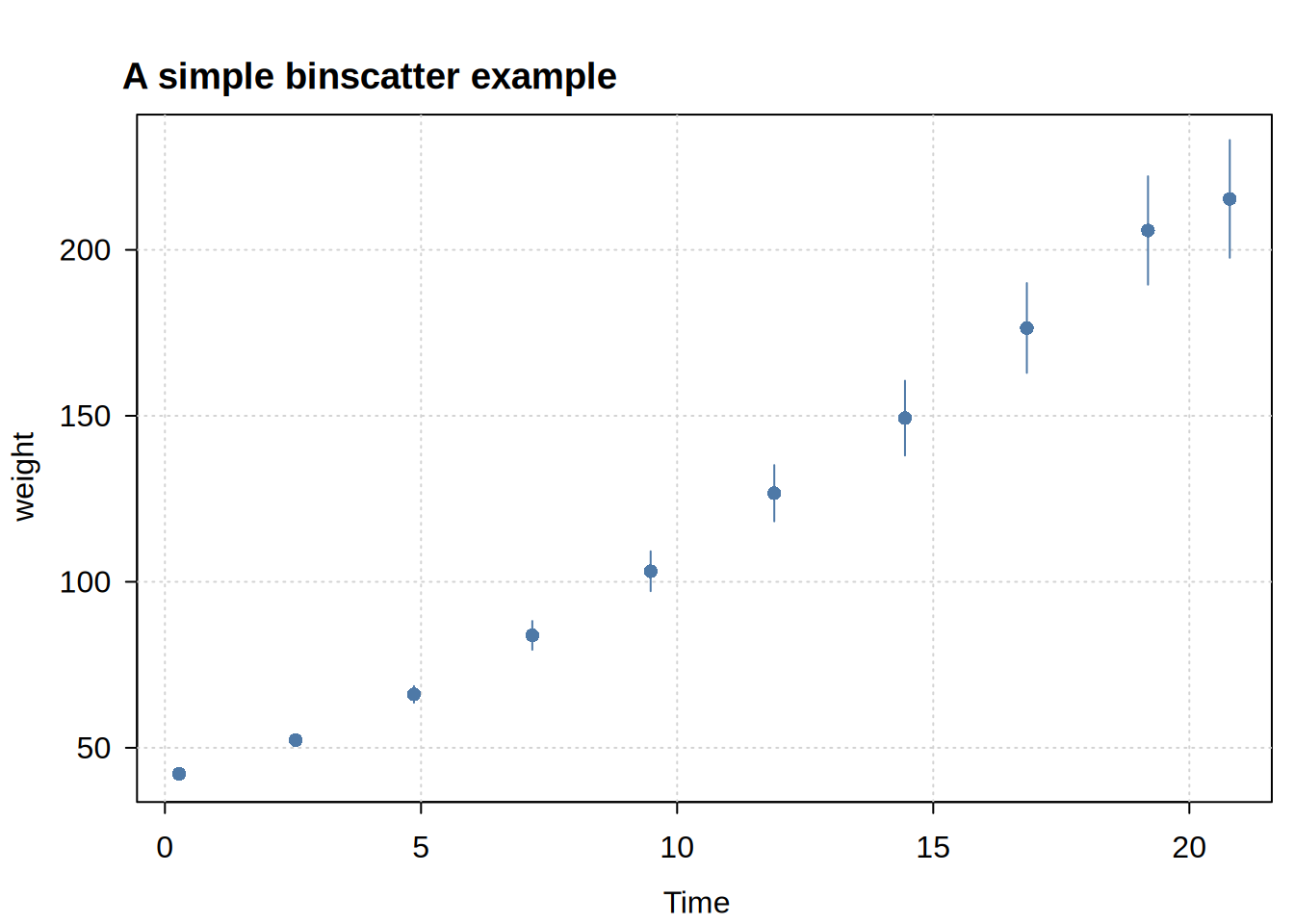
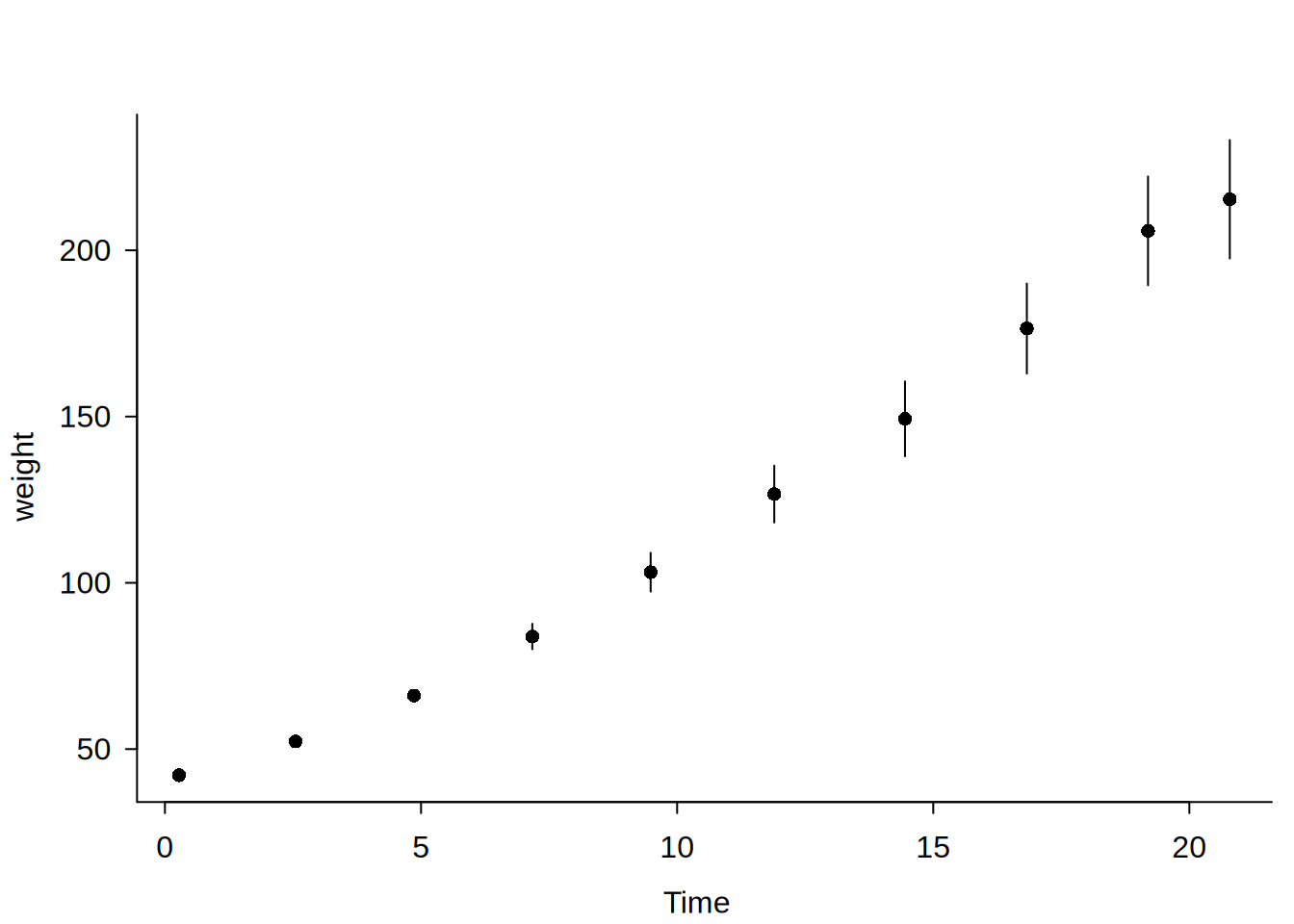
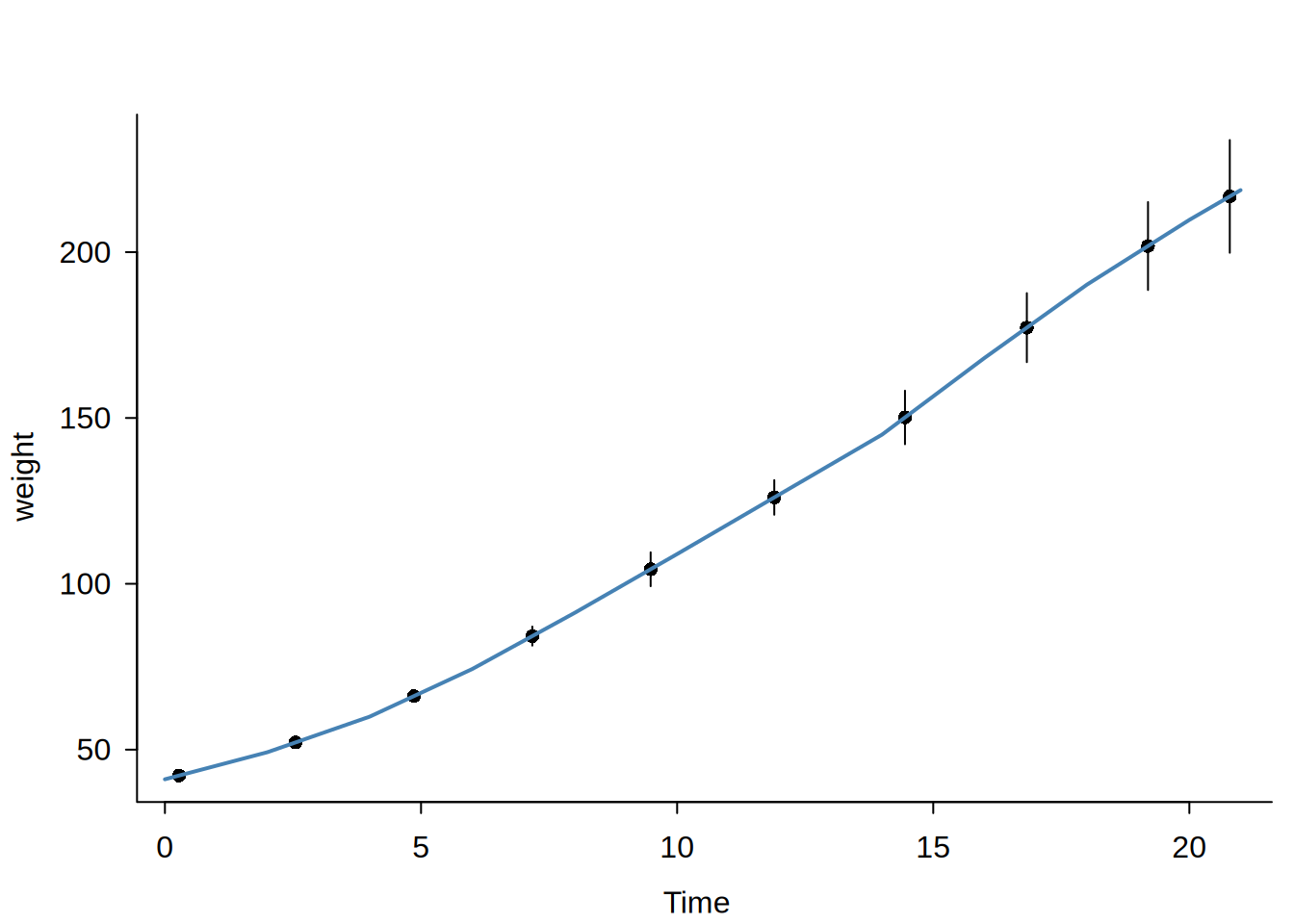
Usage
dbbinsreg(
fml,
conn = NULL,
table = NULL,
data = NULL,
path = NULL,
points = c(0, 0),
line = NULL,
linegrid = 20,
nbins = 20,
binspos = "qs",
randcut = NULL,
sample_fit = NULL,
ci = TRUE,
cb = FALSE,
vcov = NULL,
level = 0.95,
nsims = 500,
strategy = c("auto", "compress"),
plot = TRUE,
verbose = getOption("dbreg.verbose", FALSE),
dots = NULL,
...
)
Comparison with binsreg
The dbbinsreg function is deeply inspired by the binsreg package (Cattaneo et al., 2024). The main difference is that dbbinsreg performs most of its computation on a database backend, employing various acceleration strategies, which makes it particularly suitable for large datasets (which may not fit in memory). At the same time, the database backend introduces its own set of tradeoffs. We cover the most important points of similarity and difference below.
Core API and bin selection
We aim to mimic the binsreg API as much as possible. Key parameter mappings include:
Important: Unlike binsreg, dbbinsreg does not automatically select the IMSE-optimal number of bins. Rather, users must specify nbins manually (with a default of value of 20). For guidance on bin selection, see binsregselect or Cattaneo et al. (2024).
Smoothness constraints
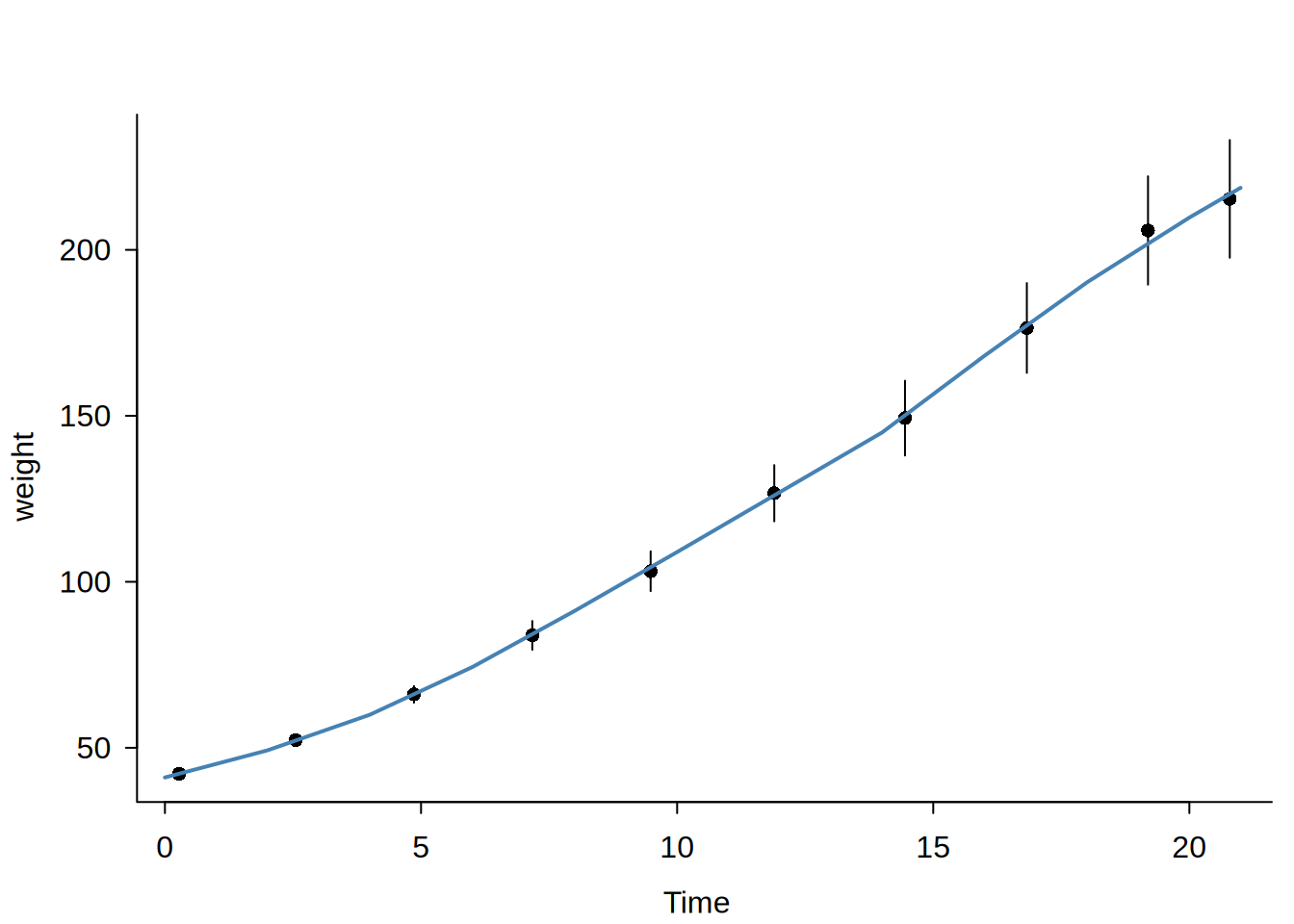
When s > 0, the function fits a regression spline using a truncated power basis. For degree \(p\) and smoothness \(s\), the basis includes global polynomial terms (\(x, x^2, \ldots, x^p\)) plus truncated power terms \((x - \kappa_j)_+^r\) at each interior knot \(\kappa_j\) for \(r = s, \ldots, p\). This enforces \(C^{s-1}\) continuity (continuous derivatives up to order \(s-1\)) at bin boundaries. For example, c(1,1) gives a piecewise linear fit that is continuous; c(2,2) gives a piecewise quadratic with continuous first derivatives.
Important: Unlike s = 0 (which uses the “compress” strategy for fast aggregation), s > 0 requires row-level spline basis construction and can be very slow on large datasets. As a result, dbbinsreg re-uses the random sample (used to compute the bin boundaries) for estimating the spline fits in these cases, ensuring much faster computation at the cost of reduced precision. Users can override this behaviour by passing the sample_fit = FALSE argument to rather estimate the spline regressions on the full dataset.
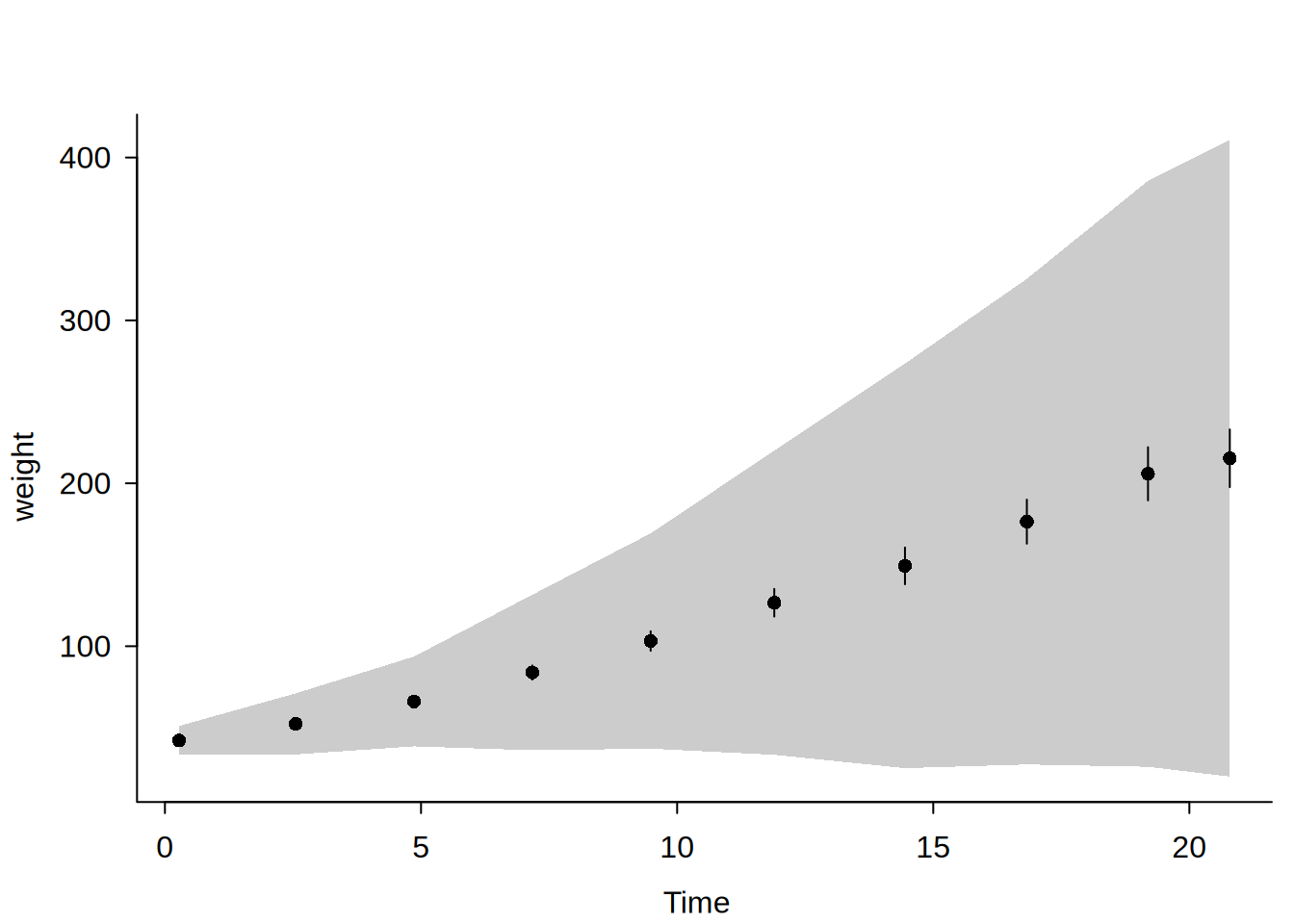
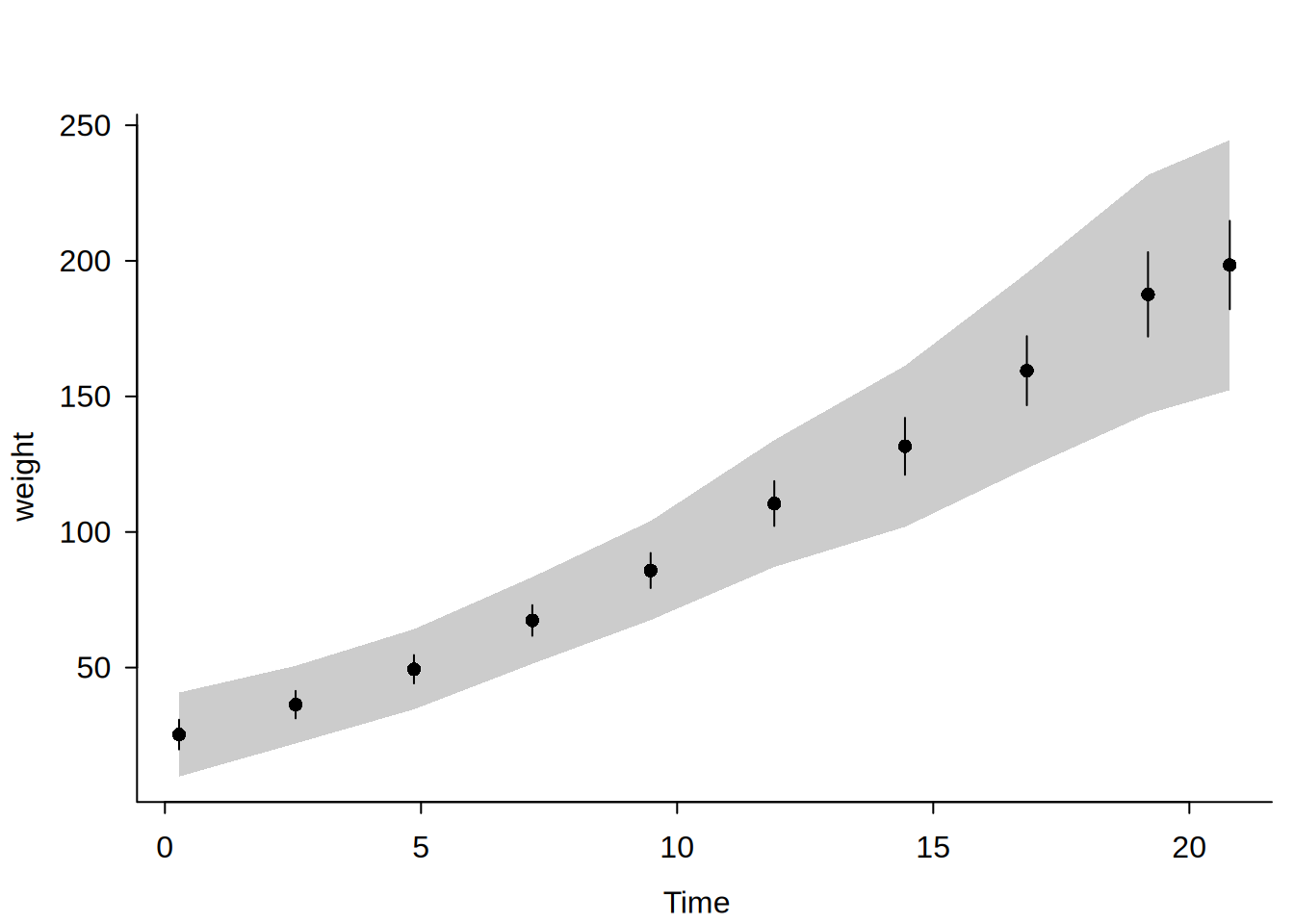
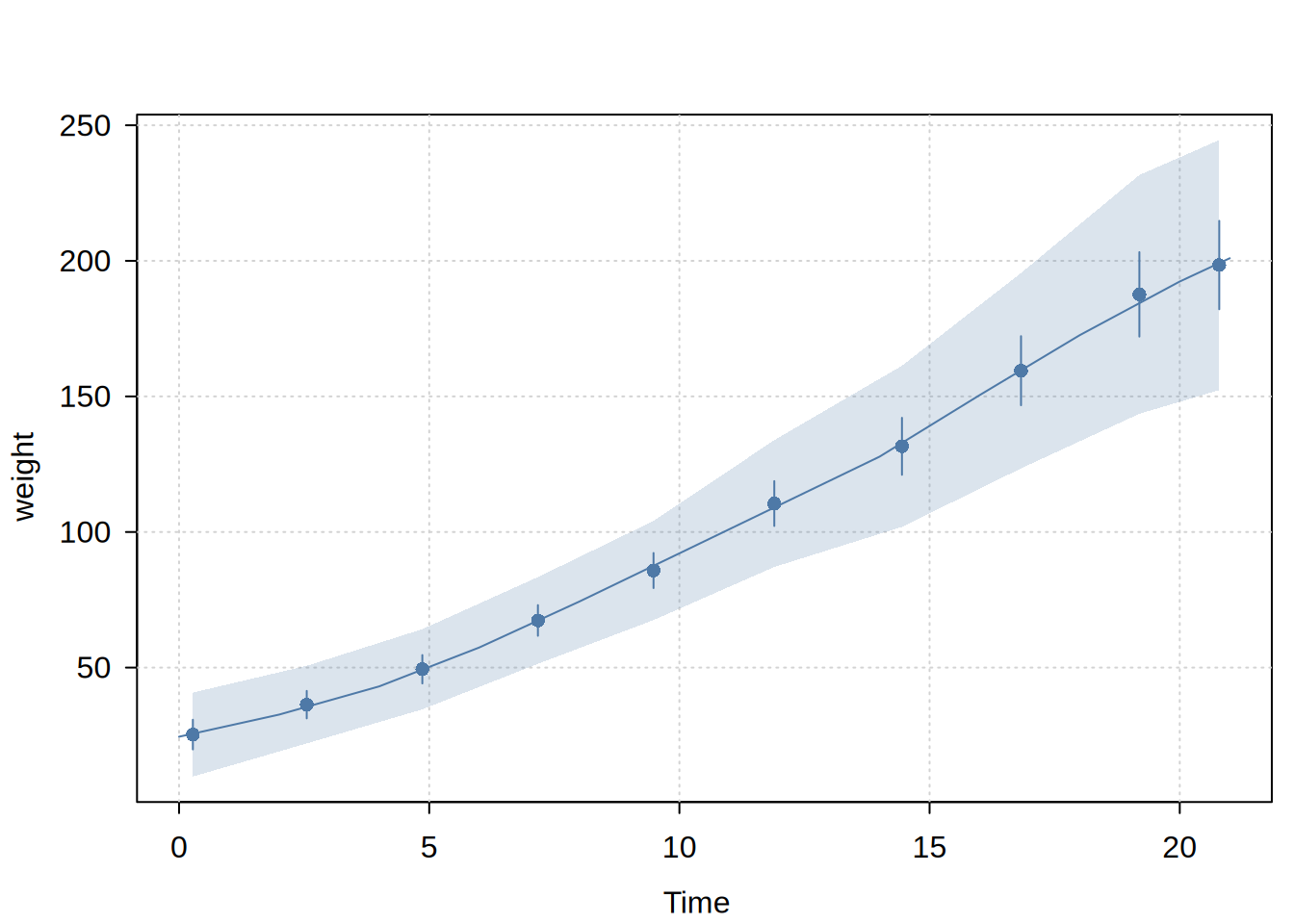
Confidence intervals vs confidence bands
When ci = TRUE (default), pointwise confidence intervals (CIs) are computed at each bin mean using standard asymptotic theory. When cb = TRUE, simultaneous confidence bands (CBs) are computed using a simulation-based sup-\(t\) procedure:
-
Draw nsims samples from the asymptotic distribution of the estimator
-
Compute the supremum of the \(t\)-statistics across all bins for each draw
-
Use the (\(1-\alpha\)) quantile of these suprema as the critical value
The confidence band is wider than pointwise CIs and provides simultaneous coverage: with (\(1-\alpha\)) probability, the entire true function lies within the band. This is useful for making statements about the overall shape of the relationship rather than individual point estimates.
There are two important caveats, regarding dbbinsreg’s CB support:
-
Unlike binsreg, which evaluates CB on a fine grid within each bin, dbbinsreg computes CB only at bin means (same points as CI). This is much simpler for our backend SQL implementation and should be sufficient for most applications.
-
CBs are currently only supported for unconstrained estimation (smoothness s = 0). When cb = TRUE with s > 0, a warning is issued and CB is skipped.
Note on quantile bin boundaries
When using quantile-spaced bins (binspos = “qs”), dbbinsreg uses SQL’s NTILE() window function, while binsreg uses R’s quantile with type = 2. These algorithms have slightly different tie-breaking behavior, which can cause small differences in bin assignments at boundaries. In practice, differences are typically <1% and become negligible with larger datasets. To match binsreg exactly, compute quantile breaks on a subset of data in R and pass them via the binspos argument as a numeric vector.