Introduction to etwfe • etwfe

Background

A canonical research design for social scientists is the so-called “difference-in-differences” (DiD) design. The essential idea behind DiD is that we can estimate the causal impact of an intervention (“treatment”) by comparing the pre- and post-intervention outcomes of indivduals that received treatment (“treated” group) against the outcomes of comparable indivduals that didn’t receive treatment (“control” group).¹

In the classic 2x2 DiD case (two units, two periods), a simple interaction effect between two dummy variables suffices to recover the treatment effect. In base R this might look something like:

lm(y ~ Dtreated_unit * Dpost_treatment, data = somedata)

where the resulting coefficient on the Dtreated_unitTRUE:Dpost_treatmentTRUE interaction term represents the treatment effect.

Rather than manually specify the interaction term, in practice researchers often use an equivalent formulation known as two-way fixed effects (TWFE). The core idea of TWFE is that we can subsume the interaction term from the previous code chunk by adding unit and time fixed effects. A single treatment dummy can then be used to capture the effect of treatment directly. A TWFE regression in base R might look as follows:

lm(y ~ Dtreat + factor(id) + factor(period), data = somedata)

where the treatment effect is now captured by the coefficient on the Dtreat dummy.

The TWFE shortcut is especially nice for more complicated panel data settings with multiple units and multiple times periods. Speaking of which, if you prefer to use a dedicated fixed effects / panel data package like fixest, you could also estimate the previous regression like so:

library(fixest)
feols(y ~ Dtreat | id + period, data = somedata)

These TWFE regressions are easy to run and intuitive, and for a long time everyone was happy. But it was too good to last. A cottage industry of clever research now demonstrates that things are not quite so simple. Among other things, the standard TWFE formulation can impose strange (negative) weighting conditions on key parts of the estimation procedure. One implication is that you risk a high probability of estimate bias in the presence of staggered treatment rollouts, which are very common in real-life applications.

Fortunately, just as econometricians were taking away one of our favourite tools, they were kind enough to replace it with some new ones. Among these, the proposed approach by Wooldridge (2021, 2023) is noteworthy. His idea might be paraphrased as stating that the problem with TWFE is not that we were doing it in the first place. Rather, it’s that we weren’t doing it enough. Instead of only including a single treatment × time interaction, Wooldridge recommends that we saturate our model with all possible interactions between treatment and time variables, including treatment cohorts, as well as other covariates. He goes on to show that this approach actually draws an equivalence between different types of estimators (pooled OLS, twoway Mundlak regression, etc.) So it’s not entirely clear what to call it. But Wooldridge refers to the general idea as as extended TWFE—or, ETWFE—which I rather like and is where this package takes its name.

The Wooldridge ETWFE solution is intuitive and elegant. But it is also rather tedious and error prone to code up manually. You have to correctly specify all the possible interactions, demean control variables within groups, and then recover the treatment effects of interest via an appropriate marginal effect aggregation. The etwfe package aims to simplify the process by providing convenience functions that do all this work for you.

Dataset

To demonstrate the core functionality of etwfe, we’ll use the mpdta dataset on US teen employment from the did package (which you’ll need to install separately).

# install.packages("did")
data("mpdta", package = "did")
head(mpdta)
#>     year countyreal     lpop     lemp first.treat treat
#> 866 2003       8001 5.896761 8.461469        2007     1
#> 841 2004       8001 5.896761 8.336870        2007     1
#> 842 2005       8001 5.896761 8.340217        2007     1
#> 819 2006       8001 5.896761 8.378161        2007     1
#> 827 2007       8001 5.896761 8.487352        2007     1
#> 937 2003       8019 2.232377 4.997212        2007     1

“Treatment” in this dataset refers to an increase in the minimum wage rate. In the examples that follow, our goal is to estimate the effect of this minimum wage treatment (treat) on the log of teen employment (lemp). Notice that the panel ID is at the county level (countyreal), but treatment was staggered across cohorts (first.treat) so that a group of counties were treated at the same time. In addition to these staggered treatment effects, we also observe log population (lpop) as a potential control variable.

Basic usage

Let’s load etwfe and work through its basic functionality. As we shall see, the core workflow of the package involves two consecutive function calls:

etwfe()
emfx()

`etwfe`

Given the package name, it won’t surprise you to learn that the key estimating function is etwfe(). Here’s how it would look for our example dataset.

library(etwfe)

mod = etwfe(
  fml  = lemp ~ lpop, # outcome ~ controls
  tvar = year,        # time variable
  gvar = first.treat, # group variable
  data = mpdta,       # dataset
  vcov = ~countyreal  # vcov adjustment (here: clustered)
)

There are a few things to say about our etwfe() argument choices and other function options, but we’ll leave those details aside until a bit later. Right now, just know that all of the above arguments are required except vcov (though I generally recommend it too, since we probably want to cluster our standard errors at the individual unit level).

Let’s take a look at our model object.

mod
#> OLS estimation, Dep. Var.: lemp
#> Observations: 2,500
#> Fixed-effects: first.treat: 4,  year: 5
#> Varying slopes: lpop (first.treat): 4,  lpop (year): 5
#> Standard-errors: Clustered (countyreal) 
#>                                               Estimate Std. Error   t value   Pr(>|t|)    
#> .Dtreat:first.treat::2004:year::2004         -0.021248   0.021728 -0.977890 3.2860e-01    
#> .Dtreat:first.treat::2004:year::2005         -0.081850   0.027375 -2.989963 2.9279e-03 ** 
#> .Dtreat:first.treat::2004:year::2006         -0.137870   0.030795 -4.477097 9.3851e-06 ***
#> .Dtreat:first.treat::2004:year::2007         -0.109539   0.032322 -3.389024 7.5694e-04 ***
#> .Dtreat:first.treat::2006:year::2006          0.002537   0.018883  0.134344 8.9318e-01    
#> .Dtreat:first.treat::2006:year::2007         -0.045093   0.021987 -2.050907 4.0798e-02 *  
#> .Dtreat:first.treat::2007:year::2007         -0.045955   0.017975 -2.556568 1.0866e-02 *  
#> .Dtreat:first.treat::2004:year::2004:lpop_dm  0.004628   0.017584  0.263184 7.9252e-01    
#> .Dtreat:first.treat::2004:year::2005:lpop_dm  0.025113   0.017904  1.402661 1.6134e-01    
#> .Dtreat:first.treat::2004:year::2006:lpop_dm  0.050735   0.021070  2.407884 1.6407e-02 *  
#> .Dtreat:first.treat::2004:year::2007:lpop_dm  0.011250   0.026617  0.422648 6.7273e-01    
#> .Dtreat:first.treat::2006:year::2006:lpop_dm  0.038935   0.016472  2.363731 1.8474e-02 *  
#> .Dtreat:first.treat::2006:year::2007:lpop_dm  0.038060   0.022477  1.693276 9.1027e-02 .  
#> .Dtreat:first.treat::2007:year::2007:lpop_dm -0.019835   0.016198 -1.224528 2.2133e-01    
#> ... 10 variables were removed because of collinearity (.Dtreat:first.treat::2006:year::2004, .Dtreat:first.treat::2006:year::2005 and 8 others [full set in $collin.var])
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> RMSE: 0.537131     Adj. R2: 0.87167 
#>                  Within R2: 8.449e-4

What etwfe() has done underneath the hood is construct a treatment dummy variable .Dtreat and saturated it together with the other variables of interest as a set of multiway interaction terms.²

You may have noticed that our etwfe() call returns a standard fixest object, since this is what it uses to perform the underlying estimation. All of the associated methods and functions from the fixest package are thus compatible with our model object. For example, we could plot the raw regression coefficients with fixest::coefplot(), or print them to a nice regression table with fixest::etable(). However, the raw coefficients from an etwfe() estimation are not particularly meaningful in of themselves. Recall that these are complex, multiway interaction terms that are probably hard to to interpret on their own. This insight leads us to our next key function…

`emfx`

If the raw etwfe coefficients aren’t particularly useful by themselves, what can we do with them instead? Well, we probably want to aggregate them along some dimension of interest (e.g., by groups or time, or as an event study). A natural way to perform these aggregations is by recovering the appropriate marginal effects. The etwfe package provides another convenience function for doing so: emfx(), which is a thin(ish) wrapper around marginaleffects::slopes().

For example, we can recover the average treatment effect on the treated (ATT) as follows.

emfx(mod)
#> 
#>     Term .Dtreat Estimate Std. Error     z Pr(>|z|)    S   2.5 %  97.5 %
#>  .Dtreat    TRUE  -0.0506     0.0125 -4.05   <0.001 14.3 -0.0751 -0.0261
#> 
#> Type:  response 
#> Comparison: TRUE - FALSE
#> Columns: term, contrast, .Dtreat, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted

In other words, our model is telling us that an increase in the minimum wage leads to an approximate 5 percent decrease in teen employment.

Beyond simple ATTs, emfx() also supports other types of aggregations via the type argument. For example, we can use type = "calendar" to get ATTs by period, or type = "group" to get ATTs by cohort groups. But the option that will probably be useful to most people is type = "event", which will recover dynamic treatment effects a la an event study. Let’s try this out and then save the resulting object, since I plan to reuse it in a moment.

mod_es = emfx(mod, type = "event")
mod_es
#> 
#>     Term event Estimate Std. Error     z Pr(>|z|)    S   2.5 %   97.5 %
#>  .Dtreat     0  -0.0332     0.0134 -2.48    0.013  6.3 -0.0594 -0.00701
#>  .Dtreat     1  -0.0573     0.0172 -3.34   <0.001 10.2 -0.0910 -0.02373
#>  .Dtreat     2  -0.1379     0.0308 -4.48   <0.001 17.0 -0.1982 -0.07751
#>  .Dtreat     3  -0.1095     0.0323 -3.39   <0.001 10.5 -0.1729 -0.04619
#> 
#> Type:  response 
#> Comparison: TRUE - FALSE
#> Columns: term, contrast, event, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high

Our event study suggests that the teen disemployment effect of a minimum wage hike is fairly modest at first (3%), but increases over the next few years (>10%). In the next section, we’ll look at ways to communicate this kind of finding to your audience.

Presentation

Plots

As of etwfe v0.5.0, we provide a native plot.emfx method for convenient visualization.

plot(mod_es)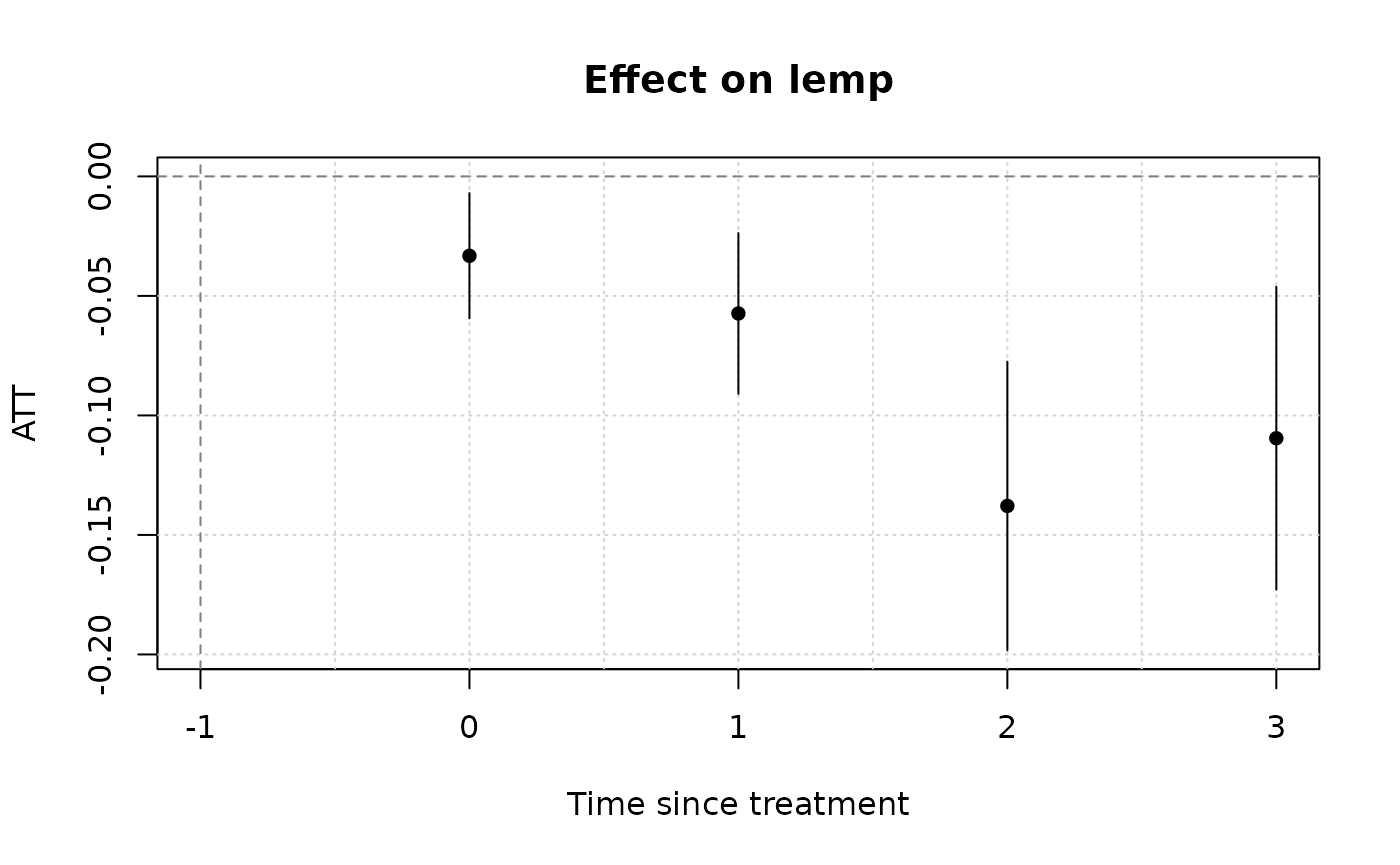

Note that emfx only reports post-treatment effects here. That’s because all pre-treatment effects have been swept out of the estimation as a result of the ETWFE setup. Specifically, under the default setting where the control group comprises the “not-yet” treated units, all pre-treatment effects are mechanistically set to zero.³ Alternatively, you can specify the “never” treated units as the control group by first calling etwfe(..., cgroup = "never"). This does return pre-treatment effects, albeit with the potential trade-off of yielding less precise estimates from not using all available information.

mod_es2 = etwfe(
  lemp ~ lpop, tvar = year, gvar = first.treat, data = mpdta, vcov = ~countyreal,
  cgroup = "never" # <= use never treated as control group
  ) |>
  emfx(type = "event")

plot(mod_es2)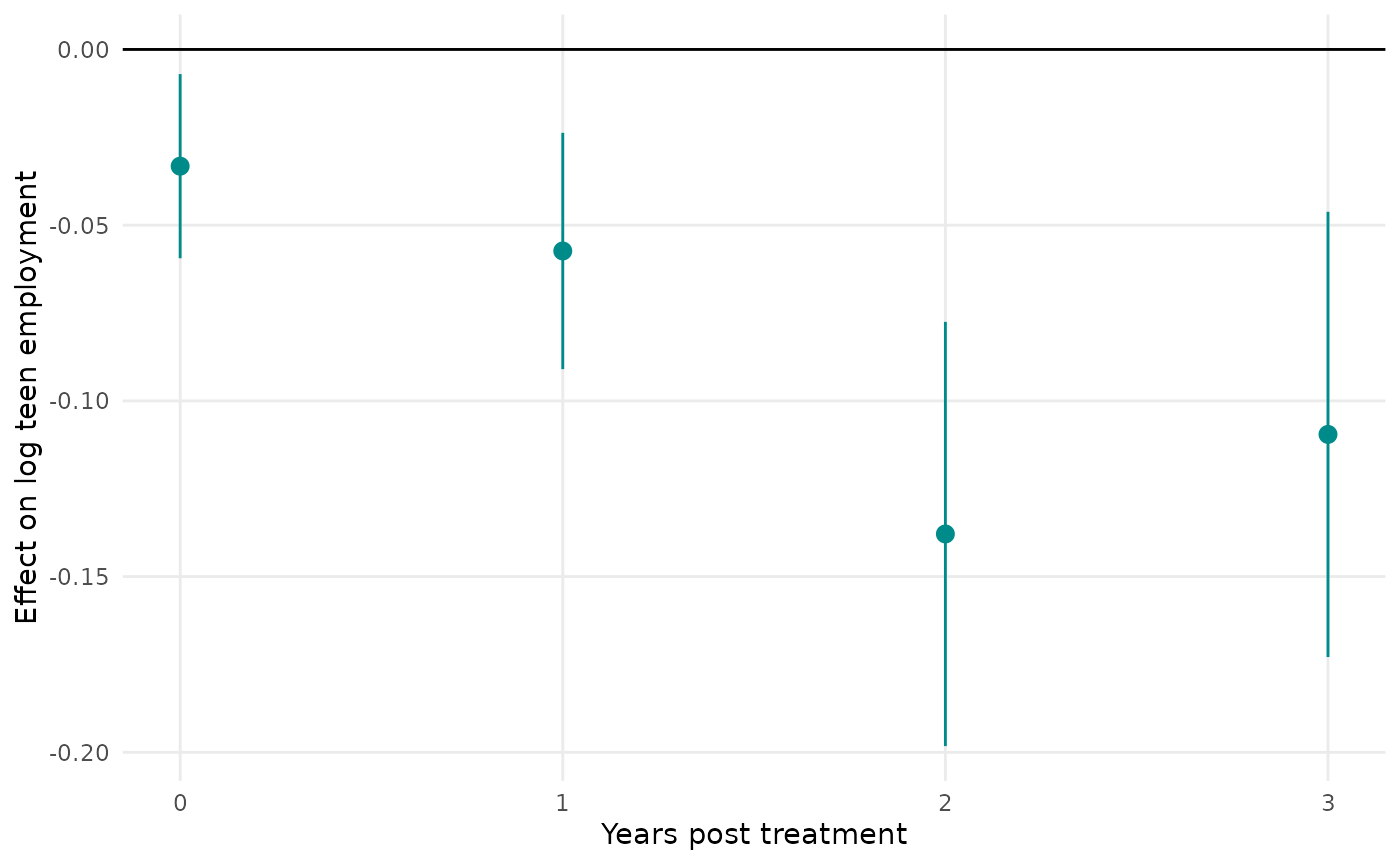

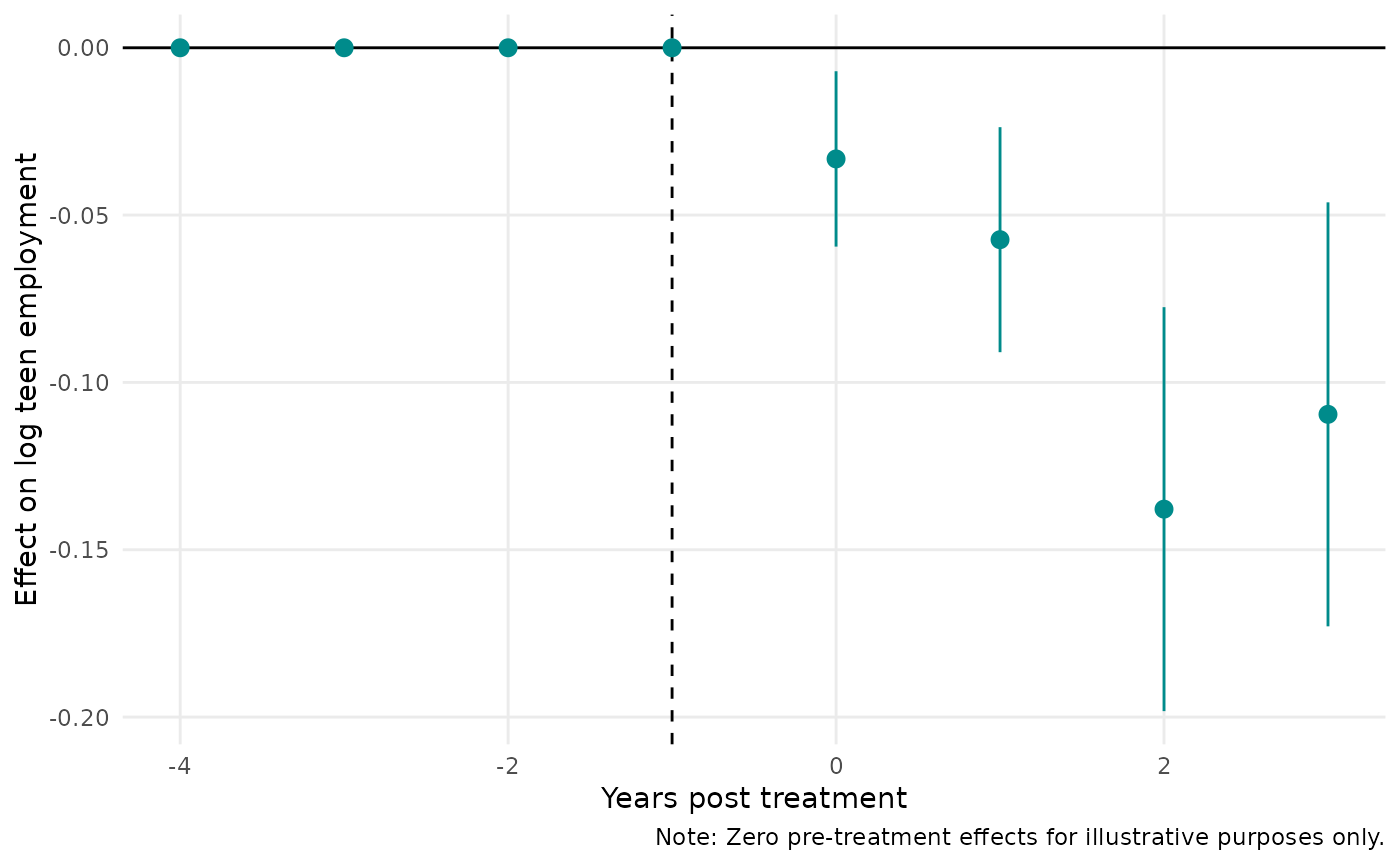
Two final points about visualizing emfx objects. First, you can customize your plots by overriding default arguments. We use tinyplot as a backend and you should be able to pass through any valid argument that tinyplot() understands. For example:

plot(
  mod_es2,
  type = "ribbon",
  col  = "darkcyan",
  xlab = "Years post treatment",
  main = "Minimum wage effect on (log) teen employment",
  sub  = "Note: Using never-treated as control group",
  # file = "event-study.png", width = 8, height = 5. ## uncomment to save file
)

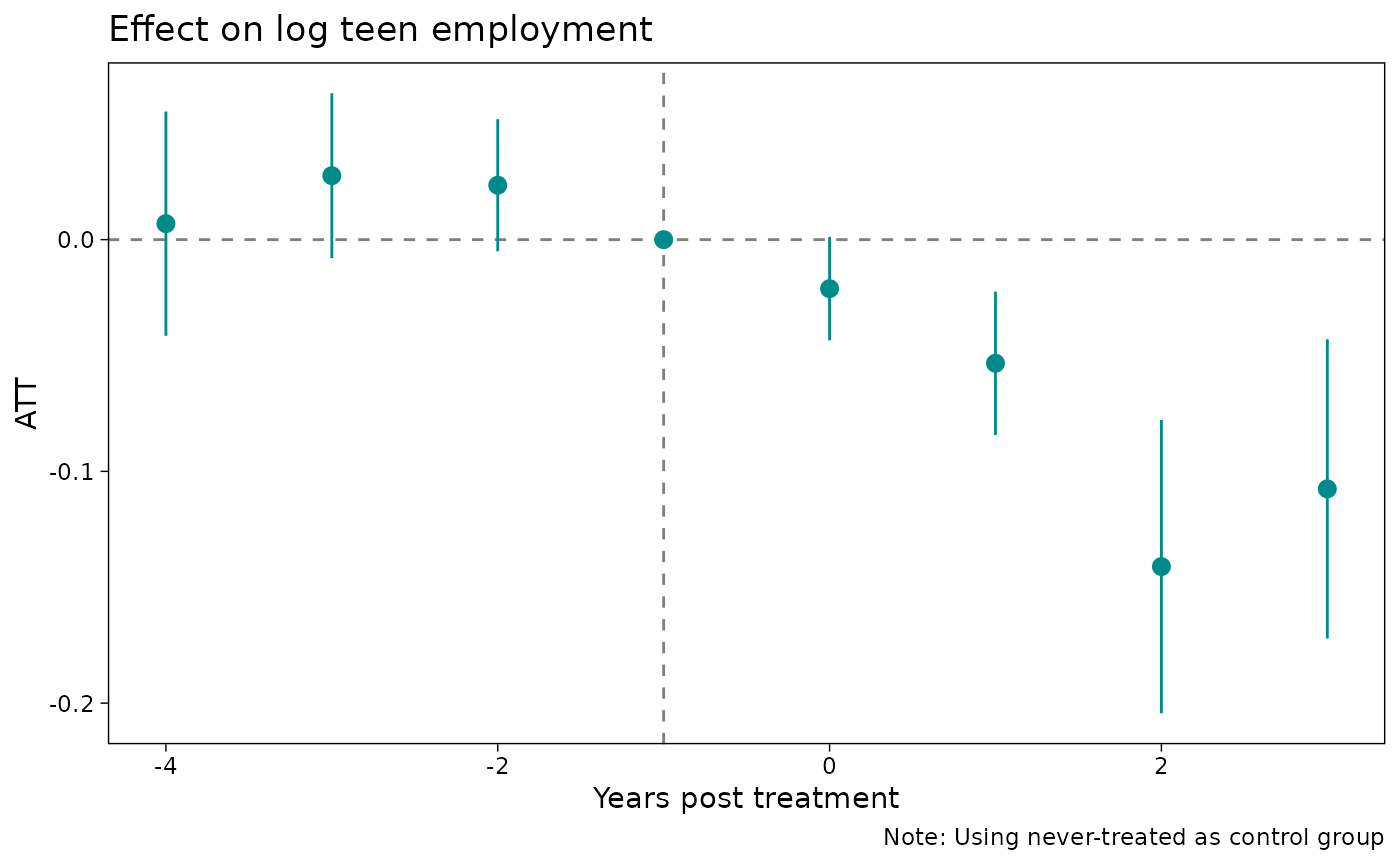
Second, since emfx objects are essentially just data.frames with additional attributes, you can easily use another plot engine if you’d prefer. For example, assuming that you have ggplot2 installed:

# install.packages("ggplot2")
library(ggplot2)
theme_set(
  theme_linedraw() + theme(panel.grid = element_blank())
)
ggplot(mod_es2, aes(x = event, y = estimate, ymin = conf.low, ymax = conf.high)) +
  geom_hline(yintercept = 0, lty = 2, col = "grey50") +
  geom_vline(xintercept = -1, lty = 2, col = "grey50") +
  geom_pointrange(col = "darkcyan") +
  labs(
    x = "Years post treatment",
    y = "ATT",
    title = "Effect on log teen employment",
    caption = "Note: Using never-treated as control group"
  )

Tables

We recommend the excellent modelsummary package for transforming your results into a nice regression table. (You will need to install it first.) Note the use of the shape and coef_rename arguments below; these are optional, but help to make the event-study output look a bit cleaner.

# install.packages("modelsummary")
library(modelsummary)

# Quick renaming function to replace ".Dtreat" with something more meaningful
rename_fn = function(old_names) {
  new_names = gsub(".Dtreat", "Years post treatment =", old_names)
  setNames(new_names, old_names)
}

modelsummary(
  list(mod_es2, mod_es),
  shape       = term:event:statistic ~ model,
  coef_rename = rename_fn,
  gof_omit    = "Adj|Within|IC|RMSE",
  stars       = TRUE,
  title       = "Event study",
  notes       = "Std. errors are clustered at the county level"
)

Event study
	(1)	(2)
+ p < 0.1, * p < 0.05, p < 0.01, * p < 0.001
Std. errors are clustered at the county level
Years post treatment = -4	0.007
	(0.025)
Years post treatment = -3	0.028
	(0.018)
Years post treatment = -2	0.023
	(0.015)
Years post treatment = -1	0.000
Years post treatment = 0	-0.021+	-0.033*
	(0.011)	(0.013)
Years post treatment = 1	-0.053***	-0.057***
	(0.016)	(0.017)
Years post treatment = 2	-0.141***	-0.138***
	(0.032)	(0.031)
Years post treatment = 3	-0.108**	-0.110***
	(0.033)	(0.032)
Num.Obs.	2500	2500
R2	0.873	0.873
FE..first.treat	X	X
FE..year	X	X

Heterogeneous treatment effects

So far we’ve limited ourselves to homogeneous treatment effects, where the impact of treatment (i.e., minimum wage hike) is averaged across all US counties in our dataset. However, many research problems require us to estimate treatment effects separately across groups and then, potentially, test for differences between them. For example, we might want to test whether the efficacy of a new vaccine differs across age groups, or whether a marketing campaign was equally successful across genders. The ETWFE framework naturally lends itself to these kinds of heterogeneous treatment effects.

Consider the following example, where we first create a logical dummy variable for all US counties in the eight Great Lake states (GLS).

gls_fips = c("IL" = 17, "IN" = 18, "MI" = 26, "MN" = 27,
             "NY" = 36, "OH" = 39, "PA" = 42, "WI" = 55)

mpdta$gls = substr(mpdta$countyreal, 1, 2) %in% gls_fips

Now imagine that we are interested in estimating separate treatment effects for GLS versus non-GLS counties. We do this simply by invoking the optional xvar argument as part of our etwfe() call.⁴ Any subsequent emfx() call on this object will automatically recognize that we want to recover treatment effects by these two distinct groups.

hmod = etwfe(
  lemp ~ lpop, tvar = year, gvar = first.treat, data = mpdta,
  cgroup = "never",
  vcov = ~countyreal,
  xvar = gls           ## <= het. TEs by gls
)

# Simple heterogeneous ATTs (could also specify `type = "event"`, etc.) 
(hmod_mfx = emfx(hmod))
#> 
#>     Term .Dtreat   gls Estimate Std. Error     z Pr(>|z|)   S  2.5 %  97.5 %
#>  .Dtreat    TRUE FALSE  -0.0519     0.0346 -1.50    0.134 2.9 -0.120 0.01598
#>  .Dtreat    TRUE  TRUE  -0.0394     0.0243 -1.62    0.105 3.3 -0.087 0.00823
#> 
#> Type:  response 
#> Comparison: TRUE - FALSE
#> Columns: term, contrast, .Dtreat, gls, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high

The above point estimates might tempt us to think that minimum wage hikes caused less teen disemployment in GLS counties than in the rest of the US on average. However, to test this formally we can invoke the powerful hypotheses infrastructure of the underlying marginaleffects package. Probably the easiest way to do this is by using b[i]-style positional arguments, where “[i]” denotes the row of the emfx() return object. Thus, by specifying hypothesis = "b1 = b2", we can test whether the ATTs from row 1 (non-GLS) and row 2 (GLS) are different from one another.

emfx(hmod, hypothesis = "b1 = b2")
#> 
#>   Term Estimate Std. Error      z Pr(>|z|)   S  2.5 % 97.5 %
#>  b1=b2  -0.0125     0.0528 -0.237    0.813 0.3 -0.116  0.091
#> 
#> Type:  response 
#> Columns: term, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high

Here we see that there is actually no statistical difference in the average disemployment effect between GLS and non-GLS counties. We can also confirm this with a quick visual inspection (note that we get an automatic legend, as well as dodged pointrange bars).

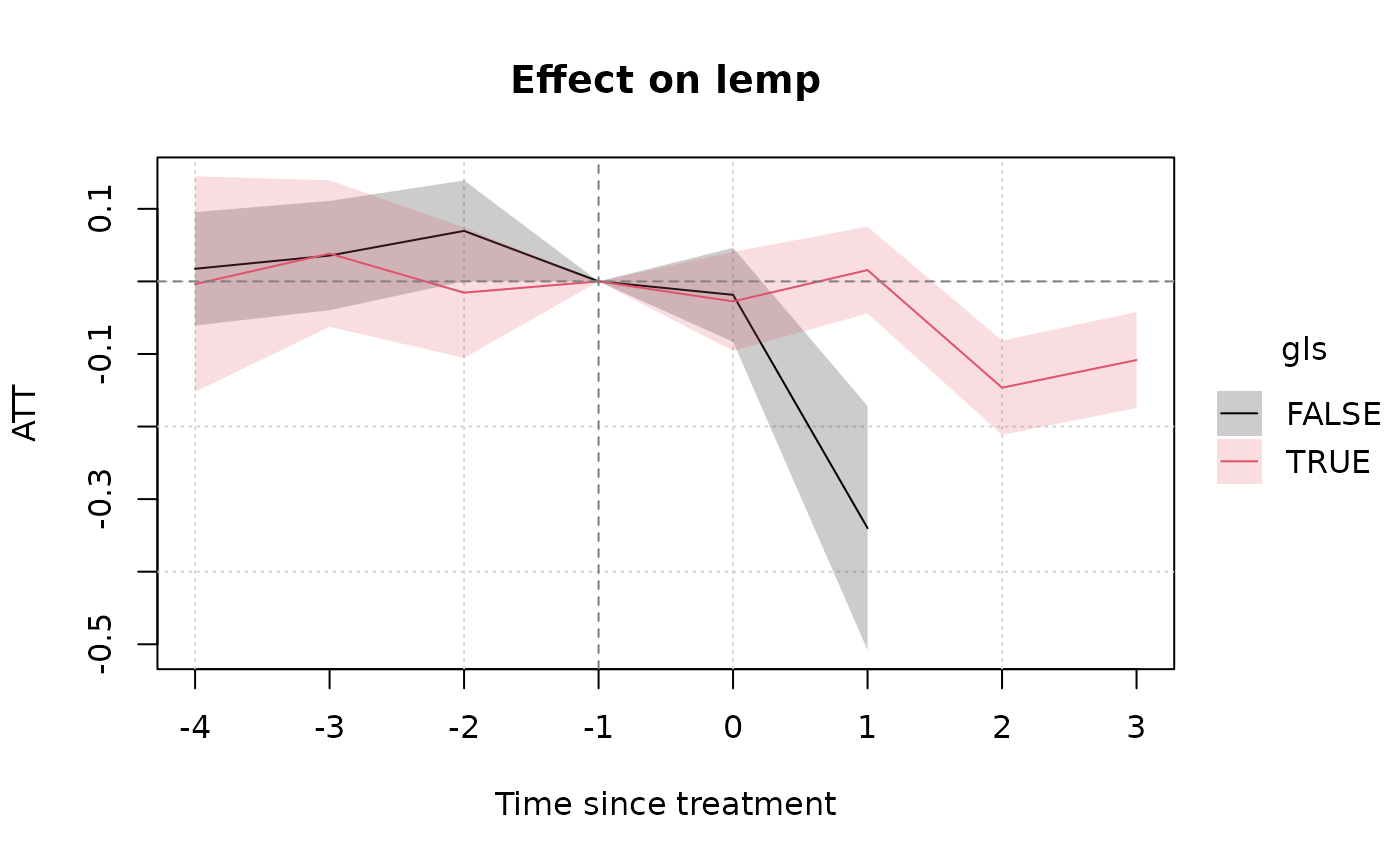
plot(hmod_mfx)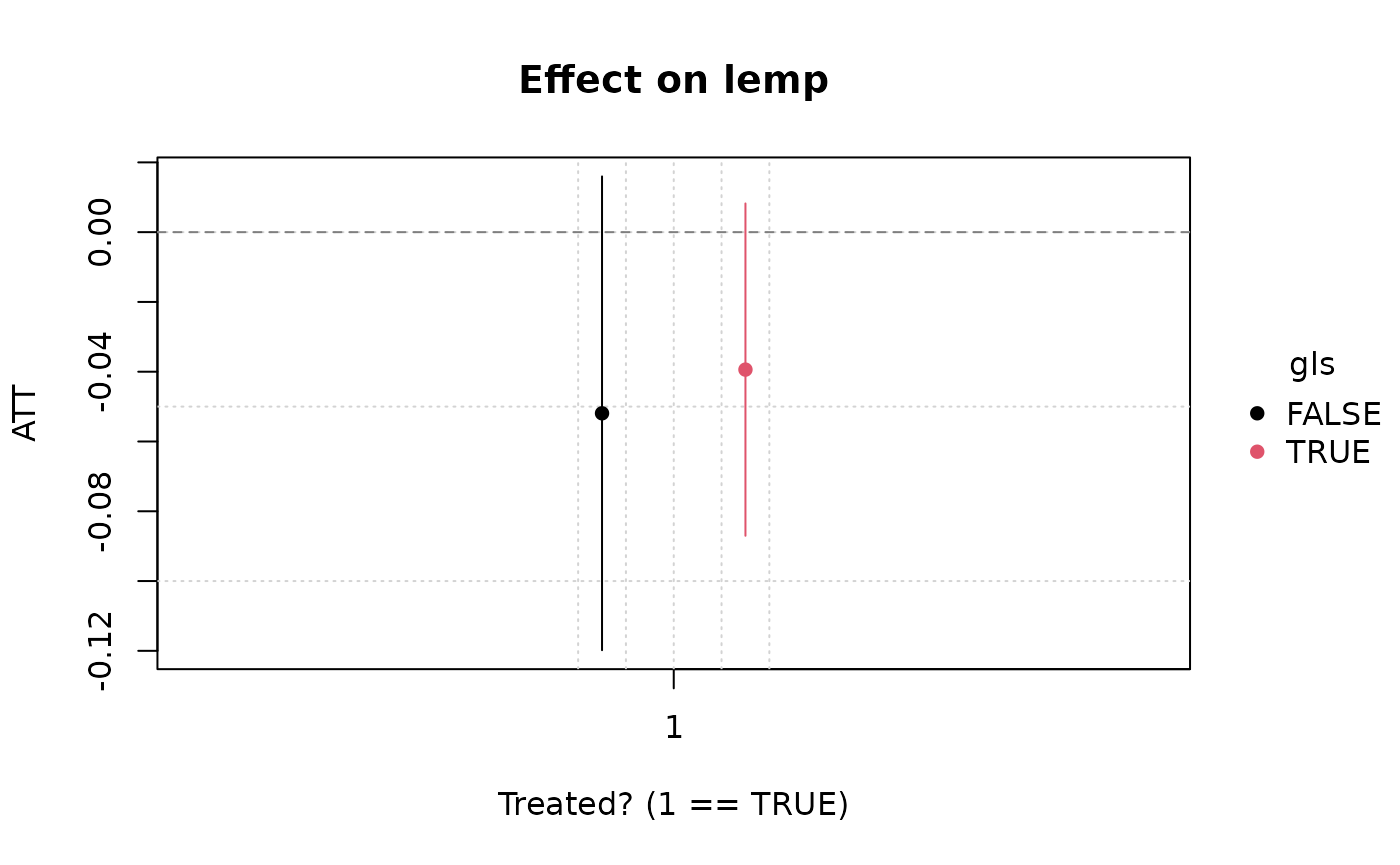

Interesting enough, however, the full event study reveals a more complex picture. Would the non-GLS counties have recorded a larger employment drop-off had we been able to collect more post-treatment data? We’ll let the the reader decide…

hmod |>
  emfx("event") |>
  plot(type = "ribbon")

One final aside is that you can easily display the results of heterogeneous treatment effects in table form too. Here’s a quick example, where we again make use of the modelsummary(..., shape = ...) argument.

modelsummary(
  models      = list("GLS county" = hmod_mfx),
  shape       = term + statistic ~ model + gls, # add xvar variable (here: gls)
  coef_map    = c(".Dtreat" = "ATT"),
  gof_map     = NA,
  title       = "Comparing the ATT on GLS and non-GLS counties"
)

Comparing the ATT on GLS and non-GLS counties
	GLS county
	FALSE	TRUE
ATT	-0.052	-0.039
	(0.035)	(0.024)

While the simple example here has been limited to a binary comparison of group
ATTs, note the same logic carries over to richer settings. We can use the exact same workflow to estimate heterogeneous treatment effects by different aggregations (e.g., event studies) and across groups with many levels.

Other families

Another key feature of the ETWFE approach—one that sets it apart from other advanced DiD implementations and extensions—is that it supports nonlinear model (distribution / link) families. Users need simply invoke the family argument. Here’s a brief example, where we recast our earlier event-study as a Poisson regression.

mpdta$emp = exp(mpdta$lemp)

etwfe(
  emp ~ lpop, tvar = year, gvar = first.treat, data = mpdta, vcov = ~countyreal,
  family = "poisson"
  ) |>
  emfx("event")
#> 
#>     Term event Estimate Std. Error       z Pr(>|z|)    S  2.5 % 97.5 %
#>  .Dtreat     0   -25.35       15.9 -1.5942    0.111  3.2  -56.5   5.82
#>  .Dtreat     1     1.09       41.8  0.0261    0.979  0.0  -80.9  83.09
#>  .Dtreat     2   -75.12       22.3 -3.3696   <0.001 10.4 -118.8 -31.43
#>  .Dtreat     3  -101.82       28.1 -3.6234   <0.001 11.7 -156.9 -46.75
#> 
#> Type:  response 
#> Comparison: TRUE - FALSE
#> Columns: term, contrast, event, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high

Performance tips

Thinking of the etwfe workflow again as a pair of consecutive functional calls, the first etwfe() stage tends to be very fast. We’re leveraging the incredible performance of fixest and also taking some shortcuts to avoid wasting time on nuisance parameters. See the Regarding fixed effects section below for more details about this.

For its part, the second emfx() stage also tends to be pretty performant. If your data has less than 100k rows, it’s unlikely that you’ll have to wait more than a few seconds to obtain results. However, emfx’s computation time does tend to scale non-linearly with the size of the original data, as well as the number of interactions from the underlying etwfe model object.⁵

Fortunately, there are two complementary strategies that you can use to speed things up. The first is to turn off the most expensive part of the whole procedure—standard error calculation—by calling emfx(..., vcov = FALSE). This should bring the estimation time back down to a few seconds or less, even for datasets in excess of a million rows. Of course, the loss of standard errors might not be an acceptable trade-off for projects where statistical inference is critical. But the good news is that we “combine” turning off standard errors with a second strategy. Specially, it turns out that compressing the data by groups prior to estimation can yield substantial speed gains on its own; see Wong et al. (2021) on this. Users can do this by invoking the emfx(..., compress = TRUE) argument. While the effect here is not as dramatic as the first strategy, collapsing the data does have the virtue of retaining information about the standard errors. The trade-off this time, however, is that compressing our data does lead to a loss in accuracy for our estimated parameters. On the other hand, testing suggests that this loss in accuracy tends to be relatively minor, with results equivalent up to the 1st or 2nd significant decimal place (or even better).

Summarizing, here is a quick plan of attack for you to try if you are worried about the estimation time for large datasets and models:

Estimate mod = etwfe(...) as per usual.
Run emfx(mod, vcov = FALSE, ...).
Run emfx(mod, vcov = FALSE, compress = TRUE, ...).
Compare the point estimates from steps 1 and 2. If they are are similar enough to your satisfaction, get the approximate standard errors by running emfx(mod, compress = TRUE, ...).

It’s a bit of performance art, since all of the examples in this vignette complete very quickly anyway. But here is a reworking of our earlier event study example to demonstrate this performance-conscious workflow.

# Step 0 already complete: using the same `mod` object from earlier...

# Step 1
emfx(mod, type = "event", vcov = FALSE)
#> 
#>     Term event Estimate
#>  .Dtreat     0  -0.0332
#>  .Dtreat     1  -0.0573
#>  .Dtreat     2  -0.1379
#>  .Dtreat     3  -0.1095
#> 
#> Type:  response 
#> Comparison: TRUE - FALSE
#> Columns: term, contrast, event, estimate

# Step 2
emfx(mod, type = "event", vcov = FALSE, compress = TRUE)
#> 
#>     Term event Estimate
#>  .Dtreat     0  -0.0332
#>  .Dtreat     1  -0.0573
#>  .Dtreat     2  -0.1379
#>  .Dtreat     3  -0.1095
#> 
#> Type:  response 
#> Comparison: TRUE - FALSE
#> Columns: term, contrast, event, estimate

# Step 3: Results from 1 and 2 are similar enough, so get approx. SEs
mod_es_compressed = emfx(mod, type = "event", compress = TRUE)

To put a fine point on it, we can can compare our original event study with the compressed estimates and see that the results are indeed very similar.

modelsummary(
  list("Original" = mod_es, "Compressed" = mod_es_compressed),
  shape       = term:event:statistic ~ model,
  coef_rename = rename_fn,
  gof_omit    = "Adj|Within|IC|RMSE",
  title       = "Event study",
  notes       = "Std. errors are clustered at the county level"
)

Event study
	Original	Compressed
Std. errors are clustered at the county level
Years post treatment = 0	-0.033	-0.033
	(0.013)	(0.013)
Years post treatment = 1	-0.057	-0.057
	(0.017)	(0.017)
Years post treatment = 2	-0.138	-0.138
	(0.031)	(0.031)
Years post treatment = 3	-0.110	-0.110
	(0.032)	(0.032)
Num.Obs.	2500	2500
R2	0.873	0.873
FE..first.treat	X	X
FE..year	X	X

Under the hood

Now that you’ve seen etwfe in action, let’s circle back to what the package is doing under the hood. This section isn’t necessary for you to use the package; feel free to skip it. But a review of the internal details should help you to optimize for different scenarios and also give you a better understanding of etwfe’s default choices.

Manual implementation

As I keep reiterating, the ETWFE approach basically involves saturating the regression with interaction effects. You can easily grab the formula of an estimated model to see for yourself.

mod$fml_all
#> $linear
#> lemp ~ .Dtreat:i(first.treat, i.year, ref = 0, ref2 = 2003)/lpop_dm
#> <environment: 0x55f6a12852a8>
#> 
#> $fixef
#> ~first.treat + first.treat[[lpop]] + year + year[[lpop]]

At this point, however, you may notice a few things. The first is that our formula references several variables that aren’t in the original dataset. An obvious one is the .Dtreat treatment dummy. A more subtle one is lpop_dm, which is the demeaned (i.e., group-centered) version of our lpop control variable. All control variables have to be demeaned before they are interacted in the ETWFE setting. Here’s how you could have constructed the dataset ahead of time and estimated the ETWFE regression manually:

# First construct the dataset
mpdta2 = mpdta |>
  transform(
    .Dtreat = year >= first.treat & first.treat != 0,
    lpop_dm = ave(lpop, first.treat, year, FUN = \(x) x - mean(x, na.rm = TRUE))
  )

# Then estimate the manual version of etwfe
mod2 = fixest::feols(
  lemp ~ .Dtreat:i(first.treat, i.year, ref = 0, ref2 = 2003) / lpop_dm |
    first.treat[lpop] + year[lpop],
  data = mpdta2,
  vcov = ~countyreal
)

We can confirm that the manual approach yields the same output as our original etwfe regression. I’ll use modelsummary to do that here, since I’ve already loaded it above.⁶.

modelsummary(
  list("etwfe" = mod, "manual" = mod2),
  gof_map = NA # drop all goodness-of-fit info for brevity
)

	etwfe	manual
.Dtreat × first.treat = 2004 × year = 2004	-0.021	-0.021
	(0.022)	(0.022)
.Dtreat × first.treat = 2004 × year = 2005	-0.082	-0.082
	(0.027)	(0.027)
.Dtreat × first.treat = 2004 × year = 2006	-0.138	-0.138
	(0.031)	(0.031)
.Dtreat × first.treat = 2004 × year = 2007	-0.110	-0.110
	(0.032)	(0.032)
.Dtreat × first.treat = 2006 × year = 2006	0.003	0.003
	(0.019)	(0.019)
.Dtreat × first.treat = 2006 × year = 2007	-0.045	-0.045
	(0.022)	(0.022)
.Dtreat × first.treat = 2007 × year = 2007	-0.046	-0.046
	(0.018)	(0.018)
.Dtreat × first.treat = 2004 × year = 2004 × lpop_dm	0.005	0.005
	(0.018)	(0.018)
.Dtreat × first.treat = 2004 × year = 2005 × lpop_dm	0.025	0.025
	(0.018)	(0.018)
.Dtreat × first.treat = 2004 × year = 2006 × lpop_dm	0.051	0.051
	(0.021)	(0.021)
.Dtreat × first.treat = 2004 × year = 2007 × lpop_dm	0.011	0.011
	(0.027)	(0.027)
.Dtreat × first.treat = 2006 × year = 2006 × lpop_dm	0.039	0.039
	(0.016)	(0.016)
.Dtreat × first.treat = 2006 × year = 2007 × lpop_dm	0.038	0.038
	(0.022)	(0.022)
.Dtreat × first.treat = 2007 × year = 2007 × lpop_dm	-0.020	-0.020
	(0.016)	(0.016)

To transform these raw coefficients into their more meaningful ATT counterparts, we just need to perform the appropriate marginal effects operation. For example, here’s how we can get both the simple ATTs and event-study ATTs from earlier. This is what emfx() is doing behind the scenes.

library(marginaleffects)

# Simple ATT
slopes(
  mod2, 
  newdata   = subset(mpdta2, .Dtreat), # we only want rows where .Dtreat is TRUE
  variables = ".Dtreat", 
  by        = ".Dtreat"
)
#> 
#>     Term .Dtreat Estimate Std. Error     z Pr(>|z|)    S   2.5 %  97.5 %
#>  .Dtreat    TRUE  -0.0506     0.0125 -4.05   <0.001 14.3 -0.0751 -0.0261
#> 
#> Type:  response 
#> Comparison: TRUE - FALSE
#> Columns: term, contrast, .Dtreat, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted

# Event study
slopes(
  mod2, 
  newdata   = transform(subset(mpdta2, .Dtreat), event = year - first.treat),
  variables = ".Dtreat", 
  by        = "event"
)
#> 
#>     Term event Estimate Std. Error     z Pr(>|z|)    S   2.5 %   97.5 %
#>  .Dtreat     0  -0.0332     0.0134 -2.48    0.013  6.3 -0.0594 -0.00701
#>  .Dtreat     1  -0.0573     0.0172 -3.34   <0.001 10.2 -0.0910 -0.02373
#>  .Dtreat     2  -0.1379     0.0308 -4.48   <0.001 17.0 -0.1982 -0.07751
#>  .Dtreat     3  -0.1095     0.0323 -3.39   <0.001 10.5 -0.1729 -0.04619
#> 
#> Type:  response 
#> Comparison: TRUE - FALSE
#> Columns: term, contrast, event, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high

Regarding fixed effects

Let’s switch gears and talk about fixed effects quickly. If you are a regular fixest user, you may have noticed that we’ve been invoking its varying slopes syntax in the fixed effect slot (i.e., first.treat[lpop] and year[lpop]). The reason for this is part practical, part philosophical. From a practical perspective, factor_var[numeric_var] is equivalent to base R’s factor_var/numeric_var “nesting” syntax but is much faster for high-dimensional factors.⁷ From a philosophical perspective, etwfe tries to limit the amount of extraneous information that it reports to users. Most of the interaction effects in the ETWFE framework are just acting as controls. By relegating them to the fixed effects slot, we can avoid polluting the user’s console with a host of extra coefficients. Nonetheless, we can control this behaviour with the fe (“fixed effects”) argument. Consider the following options and their manual equivalents.

# fe = "feo" (fixed effects only)
mod_feo = etwfe(
  lemp ~ lpop, tvar = year, gvar = first.treat, data = mpdta, vcov = ~countyreal,
  fe = "feo"
)
# ... which is equivalent to the manual regression
mod_feo2 = fixest::feols(
  lemp ~ .Dtreat:i(first.treat, i.year, ref = 0, ref2 = 2003) / lpop_dm +
    lpop + i(first.treat, lpop, ref = 0) + i(year, lpop, ref = 2003) |
    first.treat + year,
  data = mpdta2, vcov = ~countyreal
)

# fe = "none"
mod_none = etwfe(
  lemp ~ lpop, tvar = year, gvar = first.treat, data = mpdta, vcov = ~countyreal,
  fe = "none"
)
# ... which is equivalent to the manual regression
mod_none2 = fixest::feols(
  lemp ~ .Dtreat:i(first.treat, i.year, ref = 0, ref2 = 2003) / lpop_dm +
    lpop + i(first.treat, lpop, ref = 0) + i(year, lpop, ref = 2003) +
    i(first.treat, ref = 0) + i(year, ref = 2003),
  data = mpdta2, vcov = ~countyreal
)

I’ll leave it up to you to pass any of these models to emfx to confirm that they give correct aggregated treatment effects. But we can quickly demonstrate in a regression table that they all return the same raw coefficients.

mods = list(
  "etwfe"         = mod,
  "manual"        = mod2,
  "etwfe (feo)"   = mod_feo,
  "manual (feo)"  = mod_feo2,
  "etwfe (none)"  = mod_none,
  "manual (none)" = mod_none2
)

modelsummary(mods, gof_map = NA)

	etwfe	manual	etwfe (feo)	manual (feo)	etwfe (none)	manual (none)
.Dtreat × first.treat = 2004 × year = 2004	-0.021	-0.021	-0.021	-0.021	-0.021	-0.021
	(0.022)	(0.022)	(0.022)	(0.022)	(0.022)	(0.022)
.Dtreat × first.treat = 2004 × year = 2005	-0.082	-0.082	-0.082	-0.082	-0.082	-0.082
	(0.027)	(0.027)	(0.027)	(0.027)	(0.027)	(0.027)
.Dtreat × first.treat = 2004 × year = 2006	-0.138	-0.138	-0.138	-0.138	-0.138	-0.138
	(0.031)	(0.031)	(0.031)	(0.031)	(0.031)	(0.031)
.Dtreat × first.treat = 2004 × year = 2007	-0.110	-0.110	-0.110	-0.110	-0.110	-0.110
	(0.032)	(0.032)	(0.032)	(0.032)	(0.032)	(0.032)
.Dtreat × first.treat = 2006 × year = 2006	0.003	0.003	0.003	0.003	0.003	0.003
	(0.019)	(0.019)	(0.019)	(0.019)	(0.019)	(0.019)
.Dtreat × first.treat = 2006 × year = 2007	-0.045	-0.045	-0.045	-0.045	-0.045	-0.045
	(0.022)	(0.022)	(0.022)	(0.022)	(0.022)	(0.022)
.Dtreat × first.treat = 2007 × year = 2007	-0.046	-0.046	-0.046	-0.046	-0.046	-0.046
	(0.018)	(0.018)	(0.018)	(0.018)	(0.018)	(0.018)
.Dtreat × first.treat = 2004 × year = 2004 × lpop_dm	0.005	0.005	0.005	0.005	0.005	0.005
	(0.018)	(0.018)	(0.018)	(0.018)	(0.018)	(0.018)
.Dtreat × first.treat = 2004 × year = 2005 × lpop_dm	0.025	0.025	0.025	0.025	0.025	0.025
	(0.018)	(0.018)	(0.018)	(0.018)	(0.018)	(0.018)
.Dtreat × first.treat = 2004 × year = 2006 × lpop_dm	0.051	0.051	0.051	0.051	0.051	0.051
	(0.021)	(0.021)	(0.021)	(0.021)	(0.021)	(0.021)
.Dtreat × first.treat = 2004 × year = 2007 × lpop_dm	0.011	0.011	0.011	0.011	0.011	0.011
	(0.027)	(0.027)	(0.027)	(0.027)	(0.027)	(0.027)
.Dtreat × first.treat = 2006 × year = 2006 × lpop_dm	0.039	0.039	0.039	0.039	0.039	0.039
	(0.016)	(0.016)	(0.016)	(0.016)	(0.016)	(0.016)
.Dtreat × first.treat = 2006 × year = 2007 × lpop_dm	0.038	0.038	0.038	0.038	0.038	0.038
	(0.022)	(0.022)	(0.022)	(0.022)	(0.022)	(0.022)
.Dtreat × first.treat = 2007 × year = 2007 × lpop_dm	-0.020	-0.020	-0.020	-0.020	-0.020	-0.020
	(0.016)	(0.016)	(0.016)	(0.016)	(0.016)	(0.016)
lpop			1.065	1.065	1.065	1.065
			(0.022)	(0.022)	(0.022)	(0.022)
first.treat = 2004 × lpop			0.051	0.051	0.051	0.051
			(0.038)	(0.038)	(0.038)	(0.038)
first.treat = 2006 × lpop			-0.041	-0.041	-0.041	-0.041
			(0.047)	(0.047)	(0.047)	(0.047)
first.treat = 2007 × lpop			0.056	0.056	0.056	0.056
			(0.039)	(0.039)	(0.039)	(0.039)
year = 2004 × lpop			0.011	0.011	0.011	0.011
			(0.008)	(0.008)	(0.008)	(0.008)
year = 2005 × lpop			0.021	0.021	0.021	0.021
			(0.008)	(0.008)	(0.008)	(0.008)
year = 2006 × lpop			0.011	0.011	0.011	0.011
			(0.011)	(0.011)	(0.011)	(0.011)
year = 2007 × lpop			0.021	0.021	0.021	0.021
			(0.012)	(0.012)	(0.012)	(0.012)
(Intercept)					2.260	2.260
					(0.088)	(0.088)
first.treat = 2004					0.038	0.038
					(0.154)	(0.154)
first.treat = 2006					0.461	0.461
					(0.213)	(0.213)
first.treat = 2007					-0.286	-0.286
					(0.167)	(0.167)
year = 2004					-0.090	-0.090
					(0.031)	(0.031)
year = 2005					-0.110	-0.110
					(0.033)	(0.033)
year = 2006					-0.052	-0.052
					(0.040)	(0.040)
year = 2007					-0.057	-0.057
					(0.045)	(0.045)

A final point to note about fixed effects is that etwfe defaults to using group-level (i.e., cohort-level) fixed effects like first.treat, rather than unit-level fixed effects like countyreal. This design decision reflects a neat ancillary result in Wooldridge (2021), which proves the equivalence between the two types of fixed effects for linear cases. Group-level effects have the virtue of being faster to estimate, since there are fewer factor levels. Moreover, they are required for nonlinear model families like Poisson per the underlying ETWFE theory. Still, you can specify unit-level fixed effects for the linear case through the ivar argument. Again, we can easily confirm that this yields the same estimated treatment effects as the group-level default (although the standard errors will be slightly different).

mod_es_i = etwfe(
  lemp ~ lpop, tvar = year, gvar = first.treat, data = mpdta,
  ivar = countyreal  # NEW: Use unit-level (county) FEs
  ) |>
  emfx("event")

modelsummary(
  list("Group-level FEs (default)" = mod_es, "Unit-level FEs" = mod_es_i),
  shape       = term:event:statistic ~ model,
  coef_rename = rename_fn,
  gof_omit    = "Adj|Within|IC|RMSE"
)

	Group-level FEs (default)	Unit-level FEs
Years post treatment = 0	-0.033	-0.033
	(0.013)	(0.015)
Years post treatment = 1	-0.057	-0.057
	(0.017)	(0.019)
Years post treatment = 2	-0.138	-0.138
	(0.031)	(0.034)
Years post treatment = 3	-0.110	-0.110
	(0.032)	(0.036)
Num.Obs.	2500	2500
R2	0.873	0.993
FE..year	X	X
FE..first.treat	X
FE..countyreal		X