On economic “consensus” and the benefits of climate change

Richard Tol is a man who likes to court controversy. I won't deem to analyse his motivations here. Suffice it to say that I respect his professional research at the same time as I find his social media interactions maddeningly obscure, churlish and inconsistent. Still, whatever the reason, he seems to relish the the role of provocateur in the climate change debate.

Little wonder, then, that his research acts as inspiration for climate articles of a more — shall we say — considered sceptical viewpoint. By this I mean contrarian opinion pieces that at least try to marshal some credible scientific evidence in arguing their case. (As opposed to simply mouthing off the standard inanities: "It's a giant communist conspiracy", etc). For example, both Bjørn Lomborg and Matt Ridley have cited Richard's research in arguing against decisive climate action. I want to focus on Ridley today, since it will tie in nicely with something that I have discussed previously on this blog. In particular, is it true that moderate climate change will bring more benefits than harms? And, if so, is that a legitimate reason for inaction?

The basic idea is encapsulated by the following figure of Tol (2009), which shows estimates of economic damages due to temperature increases relative to the present day.

Fig. 1 Dots represent individual studies. The thick centre line is the best fit stemming from an OLS regression: \(D = 2.46T - 1.11T^2\), with an \(R^2\) value of 0.51. The outer lines are 95% confidence intervals derived according to different methods. Source: Tol (2009)

We have to be cautious in how we interpret Fig. 1. Matt Ridley might be inclined to argue (and indeed does, as we'll see below) that it shows climate change will bring society benefits long before it imposes any meaningful costs. Thus, we should do little or nothing about reducing our emissions today. There are, of course, multiple problems with this line of reasoning. I have already laid out some of the problems and complications in my previous post: sunk benefits and inertia in the climate system, uncertainty and risk aversion, unequal distribution of benefits and costs, tipping points, etc.

In today's post I am going to make two broader comments that further bolster the case against inaction. But, first, consider the following quote taken from Ridley's Spectator article of last year, "Why Climate Change Is Good For The World":

To be precise, Prof Tol calculated that climate change would be beneficial up to 2.2˚C of warming from 2009[... W]hat you cannot do is deny that this is the current consensus. If you wish to accept the consensus on temperature models, then you should accept the consensus on economic benefit.

Bold in my emphasis. Now it should be pointed out that Ridley's article has elicited various responses, including one by Bob Ward that uncovers several puzzling typos in Tol (2009). Ward goes on to show that only two out of the 14 studies considered in that paper suggest that climate change will yield any kind of net postive benefits and, moreover, that one of these two studies was borderline at best.[*] That leaves one of Richard's own papers, Tol (2002), as the sole study suggesting any kind of meaningful benefit from moderate climate change among the surveyed literature. (Tol (2002) suggests 1˚C of warming will yield a 2.3% gain in GDP.)

This is all very well-trodden ground by now, but it underscores just how tenuous — to put it mildly — Matt Ridely's appeal to economic consensus is. However, we are still left with a curve that purports to show positive benefits from climate change up until around 2˚C of warming, before turning negative. So here, then, are my two additional comments:

Comment #1: Outlier and functional form

Given that only one study among the 14 surveyed in Tol (2009) shows large-ish benefits from climate change, you may be inclined to think that the initial benefits suggested by Fig. 1 are hinged on this "outlier"... And you would not be wrong: individual observations will always stand to impact the overall outcome in small samples. However, I would also claim that such a result is partially an artefact of functional form. What do I mean by this? I mean that predicting positive benefits at "moderate" levels of warming is in some sense inevitable if we are trying to fit a quadratic function to limited data, which is exactly what Tol (2009) does. This is perhaps best illustrated by re-estimating the above figure, but (i) correcting for the typos discovered by Bob Ward and (ii) excluding the outlier in question.

Fig. 2 Based on Figure 1 in Tol (2009), but corrected for typos and including an additional best-fit line that excludes the most optimistic estimate of benefits due to moderate climate change (i.e. Tol, 2002).

Remember that our modified sample includes only negative — or neutral at best — effects on welfare due to climate change. And yet, the new best-fit line (dark grey) suggests that we will still experience net benefits for a further 1.75˚C of warming! Thus we see how the choice of a quadratic function to fit our data virtually guarantees the appearance of initial benefits, even when the data themselves effectively exclude such an outcome.[**] You'll note that I am following Ridley's lead here in ignoring the confidence intervals. This is not a particularly sound strategy from a statistical perspective, but let's keep things simple for the sake of comparison.

Comment #2: New data points

As it happens, several several new estimates of the economic effects of climate change have been made available since Tol (2009) was published. Richard has updated his Fig. 1 accordingly and included it in the latest IPCC WG2 report. You can find it on pg. 84 here. (Although — surprise! — even this is not without controversy.) However, this updated version does not include a best-fit line. That is perhaps a wise choice given the issues discussed above. Nevertheless, like me, you may still be curious to see what it looks like now that we have a few additional data points. Here I have re-plotted the data, alongside a best-fit line and 95% confidence interval.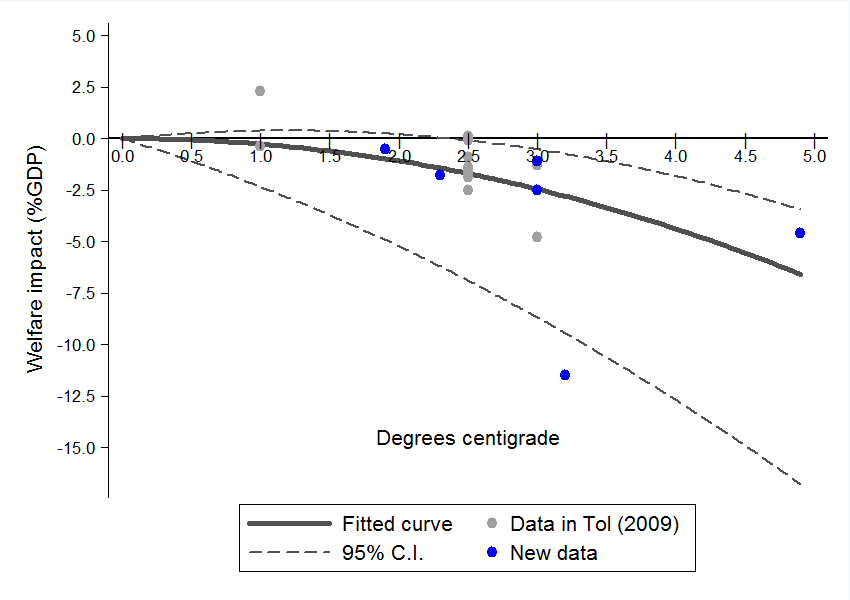

Fig. 3 Based on Figure 10 in IPCC WG2 (2014). As before, the best-fit line is computed according a quadratic function using OLS. This yields \(D = 0.01T - 0.27T^2\), with an \(R^2\) value of 0.49.

Whoops. Looks like those initial benefits have pretty much vanished! So... Anyone want to offer odds on Matt Ridley reporting the updated economic "consensus"?

UPDATE: Richard points me towards a recent working paper of his that uses non-parametric methods to fit a curve to the data. This is all well and good, and I commend his efforts in trying to overcome some of the issues discussed above... Except for one overwhelming problem: Non-parametric methods — by their very nature — are singularly ill-suited to small samples! Even Wikipedia manages to throw up a red flag in its opening paragraph on the topic: "Nonparametric regression requires larger sample sizes than regression based on parametric models because the data must supply the model structure as well as the model estimates." Arguably even more problematic is the fact that non-parametric estimations are particularly misleading in the tails. I simply don't see how a non-parametric approach can be expected to produce meaningful results, given that we are dealing with a rather pitiful 20-odd observations. Ultimately, it is not so much a question of parametric versus non-parametric. The real problem is a paucity of data.

UPDATE 2: An errata to Tol (2009) has finally been published.
UPDATE 2a: Followed by a correction to the errata! This is getting embarrassing...

UPDATE 3: Ouch and double ouch. Andrew Gelman takes Richard out to the woodshed (making many of the same points that I have here). Make sure to read the comments thread too.

___
[*] Specifically, Mendelsohn et al. (2000) suggest that 2.5˚C of warming will yield a tiny net global benefit equivalent to 0.1% of GDP. However, they do not account for non-market impacts (ecosystem services, biodiversity, etc.) which would almost certainly pull their estimate into negative territory.
[**] For the record, I don't wish to come across as overly critical about the choice of a quadratic damage function. It is hard to think of another simple function that better lends itself to describing the effect of moderate temperature increases. (Albeit not for higher levels of warming.) However, I am trying to show that limited data and the choice of functional form can combine in ways that give a misleading impression of the risks associated with climate change.