It’s not every day that you’re called an idiot by Nassim Taleb

Or a "bloggist" for that matter.

Here and here.

To be fair, Taleb has charged that many minds superior to my own are beset by idiocy, so I'm in reasonable company. More seriously, he did at least tone down his bombast when I pointed out that he had misunderstood what I was asking.

The background is this post, where I wondered (quite respectful like!) what Taleb made of the research that shows people have a tendency to overestimate the likelihood of low-probability events if they were framed in highly dramatic terms. This seemed to run counter to a recurring theme in his writings, which is that people are blind to "black swans"... basically that they consistently underestimate low-prob, high impact events.

Taleb pointed me towards a short paper on "binary" (up vs down) versus "vanilla" (+500 vs +5,000,000 vs -5,000,000) outcomes, which was supposed to refute the relevance of such studies. However, I remain rather unconvinced. Consider the key figure in my previous post:

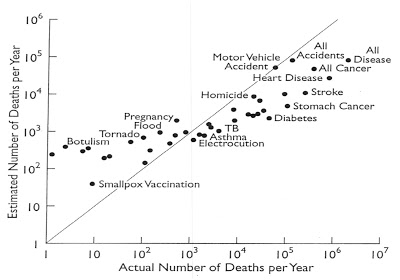Perceived versus actual fatalities. Adapted from Lichtenstein et al. (1978).

As I wrote back then: What we see here is that people have a clear tendency to overstate — by an order of several magnitudes — the relative likelihood of death arising due to "unusual and sensational" causes (tornadoes, floods, etc). The opposite is true for more mundane causes of death like degenerative disease (diabetes, stomach cancer, etc).

Now, I certainly agree with Taleb that it is important to distinguish between between binary and continuous outcomes. Asking whether a stock will go up/down is a much less interesting (and less complex) question to ask than whether it will go up/down by a certain amount. You are clearly not comparing apples with apples if you say that a stock will go up by 5% or 500%. In short, binary and continuous ("vanilla") outcomes are incommensurable in terms of evaluating payoffs.

However, the studies that I linked to are interesting exactly because they are comparing the *same* outcome (i.e. death). It makes no sense to say that death by tornado equals five times death by stroke. They are obviously equivalent. The "payoff" is thus the same because the outcome is the same. Further, I'm not claiming that the insights from these particular studies are fully generalisable to all other low probability, high-impact outcomes (especially those in finance). Yet they do show that underestimation of black swan events is hardly a universal phenomenon either... In fact, people here are shown to rely on heuristics that lead them to a diametrically opposite conclusion! I was ultimately interested in hearing from Taleb whether he thinks these heuristics are efficient or not. I didn't get an answer unfortunately, so I guess we'll have to judge for ourselves.

A final observation is that I disagree with the paper's assertion that "binary is limited to probability". (In other words, that binary outcomes say nothing about the size of a payoff.) This is certainly true in many cases — again, especially in finance — but not always. In some instances, binary outcomes imply payoffs directly. The obvious example is the one that we have been discussing in this very post, i.e. death. Indeed, I would think that Taleb probably agrees with me, given that one of his favourite analogies is that of a turkey being fattened up in preparation for Thanksgiving.

What Taleb calls his "classical metaphor". A turkey on his way to becoming dinner. (Source)

With apologies to Monty Python, you might say that the prospect of becoming an ex-turkey implies a very obvious payoff indeed.

UPDATE: Andrei Shleifer agrees.