Are there any four-minute miles in economics?

3:59.4

Roger Bannister's four laps of the Iffley Road Track on 6 May 1954 have been immortalised in the annals of sporting lore and human achievement. By becoming the first man to run a sub-four minute mile, he had broken the "impossible" barrier and so made clear the importance of mind over matter. Athletes from all over the world would soon replicate Bannister's feat now that he had liberated them from their mental shackles...

Except... no. The problem with this romantic narrative is that it has been hopelessly embellished. The idea of a four-minute "barrier" was almost entirely the invention of the media, which fanned the idea to sell papers as runners increasingly closed in on the mark. Wikipedia (indulge me) puts it quite nicely:

The claim that a 4-minute mile was once thought to be impossible by informed observers was and is a widely propagated myth created by sportswriters and debunked by Bannister himself in his memoir, The Four Minute Mile (1955). The reason the myth took hold was that four minutes was a nice round number which was slightly better (1.4 seconds) than the world record for nine years, longer than it probably otherwise would have been because of the effect of World War II in interrupting athletic progress in the combatant countries.

I was reminded of this yesterday, as my Twitter and Facebook feeds were flooded by excitable and angry complaints about the Dollar-Rand exchange rate breaching the symbolic threshold of 1:10.

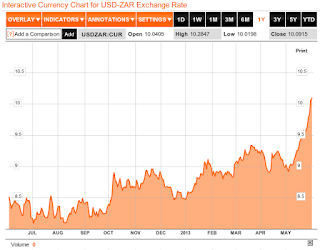Source: Bloomberg

Now, to be sure, the Rand is at it's weakest level for several years following a number of social upheavals, government scandals and political infighting, questionable economic policy, and wider trends in emerging markets. (Here, here and here for more context.) I should also say that I am not endorsing a "weak Rand" strategy here in any shape or form. I am, however, interested in the question of whether a 1:10 exchange ratio is significant in of itself.

Put differently, do we have reason to believe that the Rand's rate of depreciation will accelerate further as a result of having passed this threshold? I must confess that I don't see it. That's not to say that further depreciation can't happen, but rather: a) That would be the result of existing economic fundamentals rather than surpassing some magic metric mark, b) A full-blown currency crisis seems very unlikely from my perspective. (If nothing else, the South African Reserve Bank is on record as saying that they will tighten policy in the advent of further weakening, although that remains very open to interpretation.)

Moving beyond the case of the USD-ZAR exchange rate, the notion of thresholds pervades much of economics and finance... Or, at least, it pervades talk about economics and finance. Consider, for example, some of the headlines from recent weeks concerning the fall of gold prices to below $1,500 and then $1,400 per ounce... or the brouhaha surrounding that Rogoff-Reinhart paper and their fabled elusive "90 percent" cut-off rate for debt-to-GDP ratios and its supposedly dire consequences on economic growth.

Some of this — let's call it — threshold affinity in economics and finance could be justified by underlying factors, such as physical laws, regulatory limits, etc. However, most of it is probably just good copy for selling financial news. At worst, it may even be self-referential nonsense designed to confuse lay investors and the general public. Here are two stylised explanations for why "round number" thresholds shouldn't matter in of themselves:

1. Valuations should ultimately be set according to economic fundamentals. These would not be much different for a stock or trade that is valued at, say, R9.90 versus R10.10.
2. An alternative reason is that traders don't target levels per se. Rather, they target the levels implied by momentum and trend lines (with predefined margins of safety), or algorithmic strategies (which are similar in principle). There's no a priori reason to think that these implied levels will accord to nice round numbers.

Having said that, market psychology can obviously work very differently to the cool, rational calculations implied by standard theory. "Round numbers" will become important, as long as enough people believe them to be important. More precisely, symbolic levels will gain significance if I believe that other people regard them as being significant. (Ye old beauty contest story.) It should also be said that even standard theory does not suppose that change should evolve in a linear fashion...

Let me end this post by saying that I haven't bothered with any kind of literature research; I'd be interested in hearing about studies investigating this type of phenomena. Alternatively, if not much has been done and someone is interested in looking at it further... drop me a line. Two possibilities for checking the existence of "four-minute mile" numbers is that they should act as focal points or thresholds. For the former, we would expect data to bunch around particular levels from both above and below. For the latter, we would expect a discontinuity in the rate of change for a particular stock or currency valuation (i.e. once a threshold is breached). Several ways of testing this empirically immediately spring to mind.